Integer Programming and Hyper Sudoku
I'd like to introduce this week's guest blogger Alan Weiss. Alan writes documentation for mathematical toolboxes here at MathWorks.
Hi, folks. While I have not written a blog post for Loren before, if you use Optimization Toolbox™ or Global Optimization Toolbox then you might have read my work.
I am excited to describe how to use a new solver. Beginning with Release 2014a, Optimization Toolbox has mixed-integer linear programming. The intlinprog solver attempts to solve problems with linear objective functions, linear constraints, and (this is the new part) the constraint that some variables must be integer-valued.
The addition of integer constraints opens a surprisingly wide field of problems that are now solvable with Optimization Toolbox. There are examples in the documentation of a complicated factory production problem and solution, a travelling salesman problem, and a Sudoku puzzle solver.
This article starts with an explanation of how the Sudoku puzzle solver works. Then it extends the method to solving Hyper Sudoku puzzles. You might not be familiar with Hyper Sudoku; I will describe it presently.
Contents
Sudoku
Let's look at the Sudoku puzzle solver. As you probably know, a Sudoku puzzle is to fill a 9-by-9 grid with integers from 1 through 9 so that each integer appears only once in each row, column, and major 3-by-3 square, as in the following diagram, which includes puzzle clues.
The clues are encoded as follows: each row of a clue matrix has the form [i,j,k]. This means row i, column j, has clue k. If the first row is [1,2,2], then the clue at row 1, column 2 is equal to 2. Both the sudokuEngine and drawSudoku functions accept clues in this form, or the more conventional 9-by-9 matrix form.
B = [1,2,2;
1,5,3;
1,8,4;
2,1,6;
2,9,3;
3,3,4;
3,7,5;
4,4,8;
4,6,6;
5,1,8;
5,5,1;
5,9,6;
6,4,7;
6,6,5;
7,3,7;
7,7,6;
8,1,4;
8,9,8;
9,2,3;
9,5,4;
9,8,2];
drawSudoku(B)

The documentation shows how to solve this Sudoku puzzle using the sudokuEngine function:
drawSudoku(sudokuEngine(B));
LP: Optimal objective value is 29565.000000.
Cut Generation: Applied 1 strong CG cut,
and 2 zero-half cuts.
Lower bound is 29565.000000.
Relative gap is 0.00%.
Optimal solution found.
Intlinprog stopped at the root node because the objective value is within a gap
tolerance of the optimal value; options.TolGapAbs = 0 (the default value). The
intcon variables are integer within tolerance, options.TolInteger = 1e-05 (the
default value).

How does sudokuEngine solve Sudoku puzzles? It simply encodes the rules and clues in a binary integer programming problem. The intlinprog function does the work. Isn't that great? You don't have to figure out a solution algorithm. Compare this with several Sudoku solvers in the File Exchange and Cleve's article about how to program a Sudoku solver. Those all use ingenuity to develop a Sudoku-solving algorithm. But we don't have to figure out an algorithm. We just have to figure out how to represent the rules of Sudoku as an integer linear programming problem. sudokuEngine uses a binary integer programming formulation.
How to Model Sudoku As a Binary Integer Program
The key trick in turning the rules of Sudoku into a binary integer program is to turn the 9-by-9 grid of clues and answers into a 9-by-9-by-9 cube of binary numbers. Think of the cube as a stack of 9-by-9 grids, one at level 1, one at level 2, up to a grid at level 9. A clue of, say, 5 in the original (3,4) grid becomes a 1 at level 5 in the cube at grid coordinate (3,4). In other words, the (i,j) grid can be viewed as a stack of 9 levels, and a value k in the (i,j) grid becomes a 1 at stack level k.
RGB = imread('sudokuGrid3D.jpg'); image(RGB); axis image; axis off;
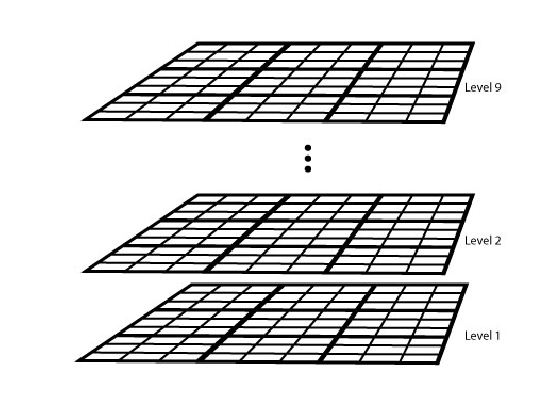
Of course, for this to make sense, the solution needs to have exactly one 1 in the stack at each grid coordinate. So if x(i,j,k) represents the value of the (i,j) grid at level k, then we must have
$$\sum_{k=1}^9 x(i,j,k) = 1$$
at a solution.
What are the other rules of Sudoku? Each row has exactly one number of each value from 1 to 9. In equations, for each $j$ and $k$, we have
$$\sum_{i=1}^9 x(i,j,k) = 1$$
Each column has exactly one number of each value, too. So for each $i$ and $k$,
$$\sum_{j=1}^9 x(i,j,k) = 1$$
Each major 3-by-3 grid has exactly one number of each type (1 through 9). For the grid elements $1\le i\le 3$ and $1\le j\le 3$, and for each $1\le k\le 9$,
$$\sum_{i=1}^3\sum_{j=1}^3 x(i,j,k) = 1.$$
To represent all nine major grids, just add 3 or 6 to each $i$ and $j$ index:
$$\sum_{i=1}^3\sum_{j=1}^3 x(i+U,j+V,k) = 1,$$
where $U,V~\epsilon~\{0,3,6\}.$
Put the Rules in intlinprog Form
The intlinprog function has a similar syntax to most Optimization Toolbox functions. The constraints on the solution x are bounds and linear equalities. All the entries in x are binary numbers, so all the lower bounds are 0 and all the upper bounds are 1.
lb = zeros(9,9,9); ub = 1 + lb;
The other constraints are all linear equalities. Optimization Toolbox solvers use the syntax
$$Aeq\cdot x = beq$$
to represent linear equalities, where x is regarded as a column vector.
x is naturally a 9-by-9-by-9 matrix. However, you can transform it to a column vector using the colon operator xcolumn = x(:). You can recover the 9-by-9-by-9 matrix representation using the reshape function: x = reshape(xcolumn,9,9,9).
Let's see how to express the first equation,
$$\sum_{k=1}^9 x(i,j,k) = 1,$$
as a matrix Aeq * x = beq. Each row of the Aeq matrix is matrix multiplied by the x matrix. This is the same as saying that entry i of beq is equal to the dot product of row i of Aeq with the vector x. So to determine the entries of row i of Aeq, make a 9-by-9-by-9 array of the multipliers of x in the equation, then turn the array into a row vector. For i and j ranging from 1 to 9, we have
temp = lb; % A zero array, 9-by-9-by-9 temp(i,j,:) = 1; % Set the coefficients of x to 1 % Then take temp(:)' as a row of Aeq
N = 9^3; % number of independent variables in x, a 9-by-9-by-9 array M = 4*9^2; % number of constraints, see the construction of Aeq Aeq = zeros(M,N); % allocate equality constraint matrix Aeq*x = beq beq = ones(M,1); % allocate constant vector of ones, beq counter = 1; for i = 1:9 % one in each depth for j = 1:9 temp = lb; % Clear temp temp(i,j,1:end) = 1; % Set each depth entry to 1 Aeq(counter,:) = temp(:)'; % Change the temp array to a row, put it in Aeq counter = counter + 1; end end
Now for the equation representing each row,
$$\sum_{i=1}^9 x(i,j,k) = 1$$
do a similar mapping from array to row of Aeq
for j = 1:9 % one in each row for k = 1:9 temp = lb; % clear temp temp(1:end,j,k) = 1; % one row in Aeq*x = beq Aeq(counter,:) = temp(:)'; % put temp in a row of Aeq counter = counter + 1; end end
Similarly, put in the column constraints.
for i = 1:9 % one in each column for k = 1:9 temp = lb; temp(i,1:end,k) = 1; Aeq(counter,:) = temp(:)'; counter = counter + 1; end end
Finally, set the coefficients for the major squares.
for U = 0:3:6 % one in each square for V = 0:3:6 for k = 1:9 temp = lb; temp(U+(1:3),V+(1:3),k) = 1; Aeq(counter,:) = temp(:)'; counter = counter + 1; end end end
Represent the Sudoku Clues
Include the initial clues in the lb array by setting corresponding entries to 1. This forces the solution to have x(i,j,k) = 1.
for i = 1:size(B,1) lb(B(i,1),B(i,2),B(i,3)) = 1; end
Solve the Sudoku Puzzle
The Aeq matrix, beq vector, and bounds lb and ub represent the rules of Sudoku and the clues. The objective function vector f is not important in this case; we just want a solution to the puzzle. We have to tell the solver that all variables are integers.
opts = optimoptions('intlinprog','Display','off'); % no exit messages intcon = 1:N; % all variables are integers f = []; % no objective function, we just want a feasible solution
Now call intlinprog to solve the puzzle.
[x,~,eflag] = intlinprog(f,intcon,[],[],Aeq,beq,lb,ub,opts);
To convert the solution to usable form, simply add up the numbers at each $(i,j)$ entry, multiplied by the depth at which the numbers appear:
if eflag > 0 % good solution x = reshape(x,9,9,9); % change back to a 9-by-9-by-9 array x = round(x); % clean up non-integer solutions y = ones(size(x)); for k = 2:9 y(:,:,k) = k; % multiplier for each depth k end S = x.*y; % multiply each entry by its depth S = sum(S,3); % S is 9-by-9 and holds the solved puzzle else S = []; end drawSudoku(S)

Hyper Sudoku
Hyper Sudoku differs from Sudoku by having more constraints. There are four 3-by-3 squares in addition to the major 3-by-3 squares that also require exactly one entry of each numeral from 1 through 9. The following image shows a Hyper Sudoku puzzle taken from Wikipedia
RGB = imread('hyperBoard.png'); % Colored squares are the new constraint regions image(RGB); axis image; axis off;

It is very easy to write the rules for Hyper Sudoku based on our work to date. There are four new constraint regions, each requiring 9 equations. So allocate a new matrix Anew, and fill it in.
Anew = zeros(4*9,N); % allocate 4*9 new rows beq = [beq;ones(4*9,1)]; % extended beq matrix
The constraints involve the 3-by-3 matrices with row and column indices 2 through 4, and also indices 6 through 8.
counter = 1; % reset counter lb = zeros(9,9,9); % reset lb to all zeros for U = [2,6] % start at 2 and 6 for V = [2,6] % for both rows and columns for k = 1:9 temp = lb; temp(U+(0:2),V+(0:2),k) = 1; Anew(counter,:) = temp(:)'; counter = counter + 1; end end end Aeq = [Aeq;Anew]; % Append Anew to Aeq
Include and Solve a Hyper Sudoku Puzzle
The Hyper Sudoku puzzle pictured above can be represented by the following matrix.
B2 = [1 8 1
2 3 2
2 8 3
2 9 4
3 5 5
3 6 1
4 6 6
4 7 5
5 2 7
5 4 3
5 8 8
6 3 3
7 5 8
8 1 5
8 2 8
8 7 9
9 1 6
9 2 9];
Include the clues in the lower bound.
for i = 1:size(B2,1) lb(B2(i,1),B2(i,2),B2(i,3)) = 1; end
Solve the puzzle.
[x,~,eflag] = intlinprog(f,intcon,[],[],Aeq,beq,lb,ub,opts); if eflag > 0 % good solution x = reshape(x,9,9,9); % change back to a 9-by-9-by-9 array x = round(x); % clean up non-integer solutions y = ones(size(x)); for k = 2:9 y(:,:,k) = k; % multiplier for each depth k end S = x.*y; % multiply each entry by its depth S = sum(S,3); % S is 9-by-9 and holds the solved puzzle else S = []; end % drawSudoku(S) % this would draw the board. But for a Hyper Sudoku figure: RGB = imread('hyperBoardSolved.png'); image(RGB); axis image; axis off;

Further experiments
The drawSudoku and sudokuEngine utilities ship with R2014a, so you can solve your own puzzles easily. However, perhaps not as easily as you might like. I also submitted an entry to the File Exchange called visualSudoku that is a visual editor for Sudoku puzzles. visualSudoku has no real code, it relies on sudokuEngine to solve puzzles, but it makes it easy to solve, save, and import Sudoku puzzles.
I also uploaded a visual Hyper Sudoku solver, and an engine for solving Hyper Sudoku puzzles.
The constraint matrices for Sudoku and Hyper Sudoku are quite sparse. I did not use that sparsity in the formulation. For examples using sparse constraint matrices, see the factory example or the travelling salesman problem in the documentation.
Did you enjoy seeing how to solve Sudoku or Hyper Sudoku puzzles with integer programming? Do you have any other types of puzzles you solve this way? Tell us about it here.
- Category:
- Fun,
- New Feature,
- Puzzles







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.