Detecting Circles in an Image
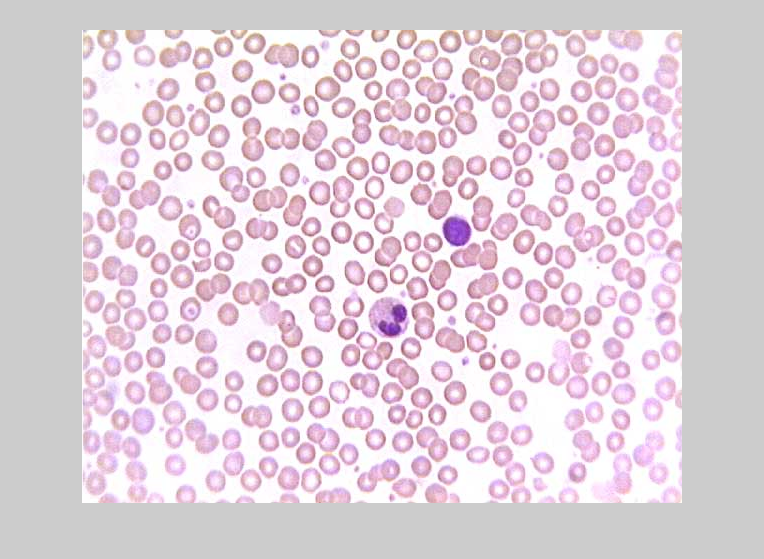
A customer recently provided me with an image of cells that were roughly circular, but not very well defined, and often overlapping.
He asked how we might use MATLAB and the Image Processing Toolbox to segment the cells in the presence of noise.
Many of us know the Hough transform functionality in the Image Processing Toolbox, and the ability of that function to detect
lines in an image. With some modifications, the Hough transform can be used to find other shapes as well. In this case, I
wanted to find circles; a quick search for "detect circles" on the MATLAB Central File Exchange revealed Tao Peng's implementation of the Circular Hough Transform. After an easy download, I was on my way to solving the problem. Tao's file is Brett's choice for this week's Pick of the Week.
(Thanks to Cem Girit at Biopticon Corp. for permission to use his image!)

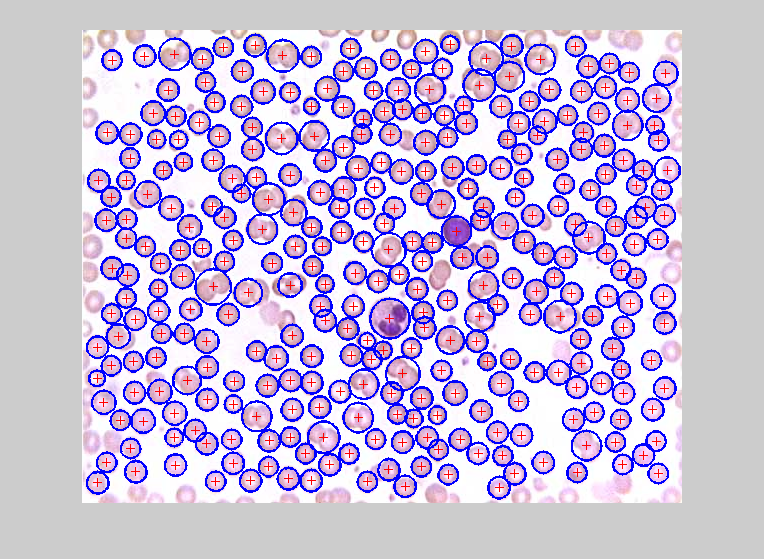 That's pretty remarkable, especially given the simplicity of my pre-processing. (Adaptive histogram equilization helped a
lot; Tao's suggested filters improve the performance even more.)
That's pretty remarkable, especially given the simplicity of my pre-processing. (Adaptive histogram equilization helped a
lot; Tao's suggested filters improve the performance even more.)
 If you do any image processing, you might recognize how Tao's function made a very challenging problem pretty manageable.
If you're not an image processing expert, this might seem a bit arcane to you...but hopefully you'll find some value in it
anyway. I'd love to hear your comments!
If you do any image processing, you might recognize how Tao's function made a very challenging problem pretty manageable.
If you're not an image processing expert, this might seem a bit arcane to you...but hopefully you'll find some value in it
anyway. I'd love to hear your comments!
Contents
Read, Display image
togglefig Original % Note: togglefig is a utility function I wrote for managing figure % windows, and is available % <https://www.mathworks.com/matlabcentral/fileexchange/loadFile.do?objectId=18220&objectType=file here>. img = imread('NB1ln1.jpg'); imshow(img);

How would you segment this?
Segmentation is often a very challenging task, particularly with noisy images like this one. One might try simple threshold or edge detection routines, or more sophisticated watershed approaches, for instance. Unfortunately, none of these approaches was giving me the results I wanted for this particular image. I was at a bit of a loss--until I found CircularHough_Grd. Tao suggests some filtering operations in his very helpful comments. For this demonstration, I'm going to see how the algorithm can perform with just some very minor pre-processing.Discarding color information
Tao's function works directly on grayscale images. Rather than converting the color image to grayscale with the Image Processing Toolbox's RGB2GRAY function, I elected to simply use the first (red) color plane, and to use adaptive histogram equalization:togglefig('Red Plane, Adjusted')
red = img(:,:,2);
red = adapthisteq(red);
imshow(red)

Parameters for the segmentation
Before I segment, I needed to know how big the cells were in the image; CircularHough_Grd takes as an input a range of radii to search for. Using the IMDISTLINE function in the Image Processing Toolbox's IMTOOL, I estimated that the radii of interest range from about 5 to 25 pixels. You can play around with the other input arguments to modify the function's sensitivity to less-than-perfect circles, for instance, or to change the way it deals with concentric circles. This makes the program pretty flexible!Now for the segmentation...
tic; [accum, circen, cirrad] = ... CircularHough_Grd(red, [5 25],... 20, 13, 1); toc
Elapsed time is 4.169272 seconds.
...and a bit of post-processing
Note to Tao: occasionally, your algorithm returns zero-radii "hits":any(cirrad <= 0)
ans =
1
This is easy to address (for instance, to keep the RECTANGLE command below from erroring), but might be an opportunity for
enhancement.
if any(cirrad <= 0) inds = find(cirrad>0); cirrad = cirrad(inds); circen = circen(inds,:); end
View the results
Now let's see how well the algorithm performed:togglefig Results imshow(img); hold on; plot(circen(:,1), circen(:,2), 'r+'); for ii = 1 : size(circen, 1) rectangle('Position',[circen(ii,1) - cirrad(ii), circen(ii,2) - cirrad(ii), 2*cirrad(ii), 2*cirrad(ii)],... 'Curvature', [1,1], 'edgecolor', 'b', 'linewidth', 1.5); end hold off;
 That's pretty remarkable, especially given the simplicity of my pre-processing. (Adaptive histogram equilization helped a
lot; Tao's suggested filters improve the performance even more.)
That's pretty remarkable, especially given the simplicity of my pre-processing. (Adaptive histogram equilization helped a
lot; Tao's suggested filters improve the performance even more.)
Final comments
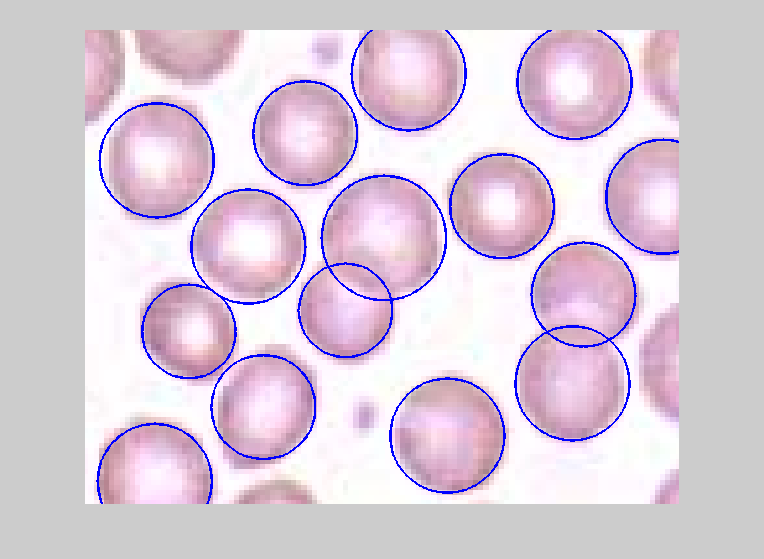
The time it takes to run this algorithm varies markedly, depending on the user settings. In this case, it took my computer approximately 4 seconds--but did a pretty amazing job of segmentating the image. Note how well it handled overlapping cells (circles), for instance:togglefig Blowup imshow(img) xlims = [406 520]; ylims = [52 143]; set(gca,'xlim',xlims,'ylim',ylims) inImageCircles = find(inpolygon(circen(:,1), circen(:,2), xlims([1 2 2 1]), ylims([1 1 2 2]))); for ii = 1 : numel(inImageCircles) rectangle('Position',... [circen(inImageCircles(ii),1) - cirrad(inImageCircles(ii)),... circen(inImageCircles(ii),2) - cirrad(inImageCircles(ii)),... 2*cirrad(inImageCircles(ii)),... 2*cirrad(inImageCircles(ii))],... 'Curvature', [1,1], 'edgecolor', 'b', 'linewidth', 1.5); end
 If you do any image processing, you might recognize how Tao's function made a very challenging problem pretty manageable.
If you're not an image processing expert, this might seem a bit arcane to you...but hopefully you'll find some value in it
anyway. I'd love to hear your comments!
If you do any image processing, you might recognize how Tao's function made a very challenging problem pretty manageable.
If you're not an image processing expert, this might seem a bit arcane to you...but hopefully you'll find some value in it
anyway. I'd love to hear your comments!
- Category:
- Picks








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.