Distance from Points to Polyline or Polygon
Sean‘s pick this week is Distance from points to polyline or polygon by Michael Yoshpe.
I recently had a problem where I was trying to identify which corners of a property lot were abutting a street.
Below is an example; the polygons are stored in the relatively new polyshape class.
load Polyshapes.mat p(1) = plot(lot, "FaceColor", "b"); hold on p(2) = plot(street, "FaceColor", [0.5 0.5 0.5]); xticks([]) yticks([]) legend(["Lot" "Street"])
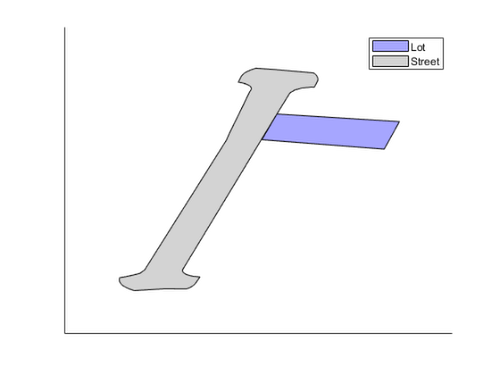
I looked at the methods for polyshape and first thought nearestvertex would be the correct way to do it. I.e. given the nearest vertex for each point, calculate the distance to it and apply a threshold.
nidx = nearestvertex(street, lot.Vertices); p(3) = plot(street.Vertices(nidx, 1), street.Vertices(nidx, 2), "r*", "DisplayName", "Nearest Vertex on Street");
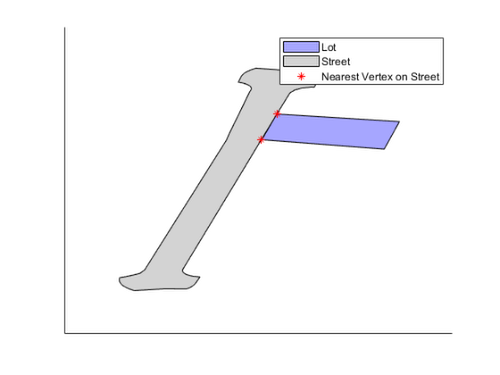
At first this looks good, but let’s zoom in:
load zoomlimits.mat
xlim(xlimits)
ylim(ylimits)
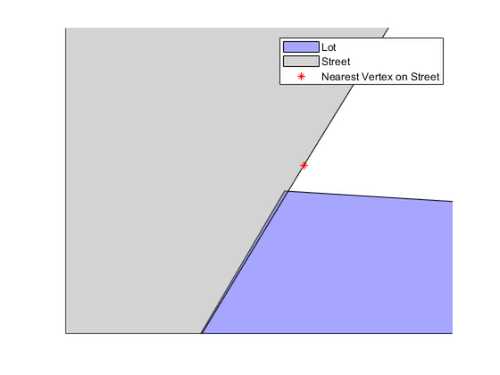
Nearest vertex is only looking at the vertices for a street. There can be long distances between the vertices along a boundary so it could return ones that make absolutely no sense e.g. the far side of the street. What I actually need is the distance from the lot vertices to the boundaries of the street.
Unfortunately, there was no obvious polyshape method in a computational geometry sense to do it. I could use linspace to add thousands of points to each boundary to up the number of vertices so nearestvertex could get “close enough” but that seemed like a less than optimal means for solving this problem.
I searched MATLAB Answers and came across this answer from MathWorks’ Tech Support. This provided a means for finding distance to a line. One could loop over all of the boundaries of the street, calculate the shortest distance, and then keep the minimum at the end. Instead, I searched the File Exchange and found Michael’s p_poly_dist function. It does exactly what I need (though requires looping over vertices instead of boundaries).
% Grab the boundary from the street. [xbnd, ybnd] = boundary(street); % Loop over lot vertices, calculating shortest distance to street boundary. for ii = size(lot.Vertices, 1):-1:1 dists(ii, 1) = p_poly_dist(lot.Vertices(ii, 1), lot.Vertices(ii, 2), xbnd, ybnd); end % A vertex is on the border if it's within threshold or street interior. threshold = 2; onborder = (dists < threshold) | isinterior(street, lot.Vertices); delete(p(3)) plot(lot.Vertices(onborder, 1), lot.Vertices(onborder, 2), "mp", "DisplayName", "On Street") xlim auto ylim auto
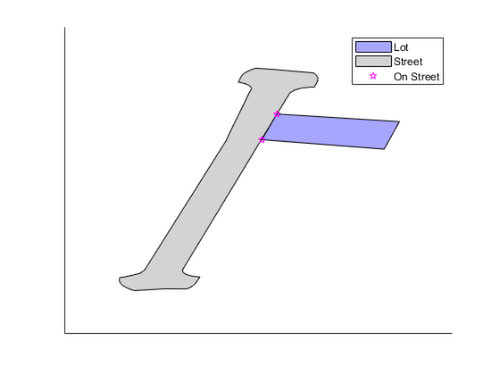
I’d also like to give a shout out to Point To Line Distance by Rik Wisselink – who provided input checking to the tech support answer and extended it to work on multiple points. I didn’t use it for this because I did not need 3d and looping over boundaries was many more iterations than looping over vertices.
Comments
If you want this functionality in base MATLAB, please contact MathWorks Tech Support and add your vote by letting them know this answer was useful!
Give it a try and let us know what you think here or leave a comment for Michael.
Published with MATLAB® R2019a
- カテゴリ:
- Picks








コメント
コメントを残すには、ここ をクリックして MathWorks アカウントにサインインするか新しい MathWorks アカウントを作成します。