Minimal Bounding Box
Sean‘s pick this week is Minimal Bounding Box by Johannes Korsawe.
I was recently asked by a customer “How can I replicate the flatness measurements from a CMM machine?” A coordinate measuring machine measures geometric properties of an object.
A quick internet search, took me to this site which introduced two methods. The customer wanted the “Minimum Zone” method, sometimes also referred to as parallel planes. This essentially boils down to “fit a minimum bounding box and calculate the distance between the top and bottom of the box”.
I knew it must be possible to to formulate this as an optimization routine whether something linear that linprog could handle or nonlinear with linear constraints enforcing for fmincon. A quick search of the File Exchange yielded Johannes’ file which does exactly what was needed. It also provides a plotting routine to help validate and understand the output.
Here’s an example of what worked, using random numbers in place of the CMM measurements.
npts = 10; % Number of points from CMM machine. x = randi(100, npts, 1)+randn(npts, 1); y = randi(100, npts, 1)+randn(npts, 1); z = rand(npts, 1); [~, cornerpts] = minboundbox(x, y, z); scatter3(x, y, z); hold on plotminbox(cornerpts, 'r');
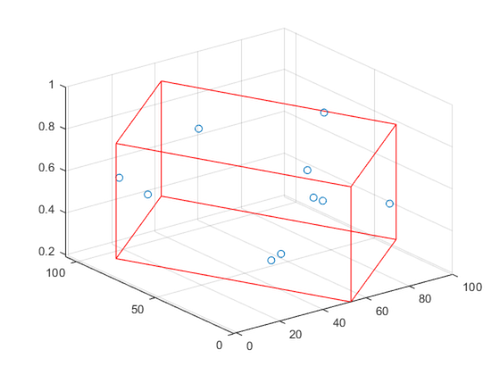
To calculate flatness, I just need to calculate the distance between a top and bottom point. I wasn’t sure if the point order was deterministic so it’s easier to just calculate the closest point on the opposite plane from a chosen one.
bottompt = cornerpts(1,:); [~, topidx] = min(hypot(cornerpts(2:end,1)-bottompt(1), cornerpts(2:end,2)-bottompt(2))); toppt = cornerpts(topidx+1,:); hold on scatter3(bottompt(1), bottompt(2), bottompt(3), 'b*') scatter3(toppt(1), toppt(2), toppt(3), 'g*')
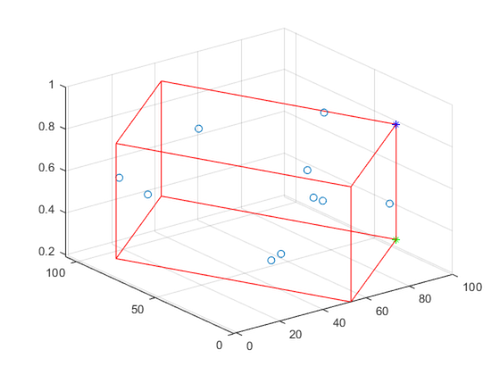
Computing the distance can be done with a couple calls to hypot.
planesep = hypot(hypot(toppt(1)-bottompt(1), toppt(2)-bottompt(2)), toppt(3)-bottompt(3));
disp("Plane separation is: " + planesep)
Plane separation is: 0.55053
Comments
Give it a try and let us know what you think here or leave a comment for Johannes.
Published with MATLAB® R2019b
- Category:
- Picks








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.