Brett's Pick this week is Ellipse Detection Using 1D Hough Transform, by Martin Simonovsky.

Contents

Introduction

I've written several times in the past about detecting circles in images (here, here, and here). I've written, too, on drawing ellipses. Today, I want to write about detecting ellipses.

Since ellipses are described by more parameters than are lines or circles, detecting ellipses is more challenging than is detecting lines or circles. And while we have nice functionality for detecting the simpler shapes (houghlines, imfindcircles), we do not (currently) have a function to detect ellipses. Enter Martin's ellipse-detection function.

The Source

Fortunately, and appropriately, Martin cited the source for his algorithm; he used a paper (Y. Xie, Q. Ji. "A New Efficient Ellipse Detection Method." 1051-4651/02 IEEE, 2002) that I have had on my desk for quite some time, thinking that I would one day sit down to implement it in MATLAB code. I love that Martin did that work for me--it makes me appreciate the File Exchange all the more.

The Implementation

After playing around with Martin's ellipseDetection() for most of an afternoon, I have some thoughts to share. First, recognize that ellipse detection is an expensive memory hog; the computation scales with the square of the number of nonzero pixels, N, in your search image. You'll almost certainly want to operate on an "edge image" rather than a simple binary mask of your regions of interest, and to play with the function's nine input parameters to limit the search. Among these parameters, you can specify the range of major axes lengths to consider, and the minimum aspect ratio. You may also specify some parameters for limiting the angles of the ellipses you seek; this could be very useful if you know the ellipse orientations a priori. Even after such limits are used, an exhaustive search examines N x N candidates for major axes. Martin's function provides a parameter that allows you to trade off between speed and accuracy. (The "randomize" parameter is not a Boolean variable, as the name suggests; rather it reduces the search space from N x N to N x randomize. If randomize is 0, then the search is exhaustive--increased accuracy at a computational cost.)

A Test Drive

So let's try it out on a sample image of our creation. We can start with an image containing circles, and warp it to generate ellipses:

inputImage = imread('coloredChips.png');
tform = affine2d([1 0 0; 0.75 1 0; 0 0 1]);
inputImage = imwarp(inputImage, tform);
imshow(inputImage)
title("Test Image")

Segmentation

I segmented the image by:

In just a few minutes, I had an edge image in which to detect those ellipses:

Detecting the Ellipses

With this binary edge mask in hand, I was ready to search for ellipses--first, naively:

bestFits = ellipseDetection(edgeMask);

The operation completed in (just) less than a second, but the results were underwhelming:

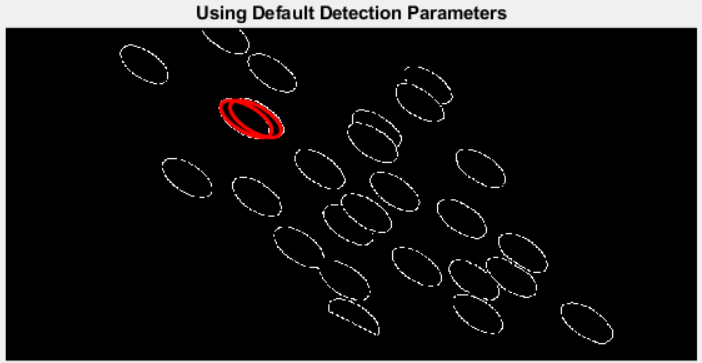
(By the way, calling ellipseDetection() on the binary mask of the warped chips without first calculating the edges took upwards of 20 minutes, and the results were even worse!)

Improving the Results

To improve the performance, I judiciously selected input parameters to reduce the computational cost. First, I used imdistline to measure the major and minor axes lengths:

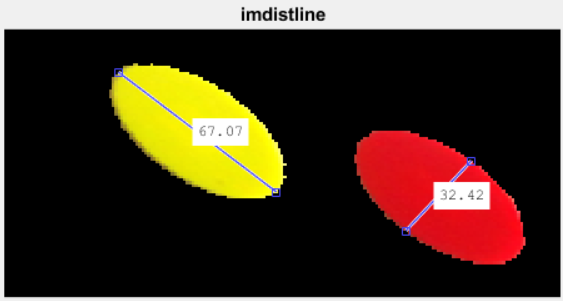
Then I used protractor to get a sense of the orientations of the ellipses:

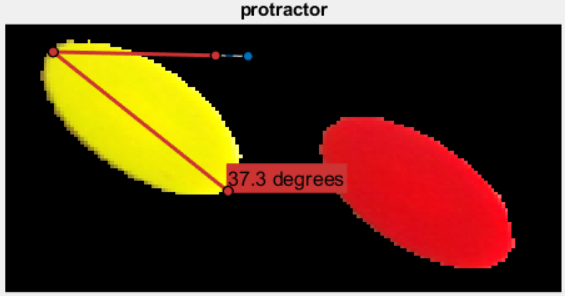
After a few minutes, I found my way to:

params.minMajorAxis = 55;
params.maxMajorAxis = 75;
params.minAspectRatio = 0.4; %1 = circle; 0 = line;
params.rotation = 35;
params.rotationSpan = 10;
params.randomize = 0; %Exhaustive search
params.numBest = 30; %(Number of chips = 26)

bestFits = ellipseDetection(edgeMask, params);

Paring Results

Wait...what? bestFits contains paramaters for 30 detections (a manual count informs me that there are 26 ellipses wholly contained in the image), but when visualizing the results, it appears that there are far fewer. What's going on?

It turns out that the algorithm is susceptible to reporting the same ellipse multiple times. (If I drag those cyan ellipses, there are other coincident ellipses underneath!)

Experimenting, I found it quite useful to dramatically overspecify the number of ellipses I wanted to detect, then to pare the results in post-processing. Consider:

params.smoothStddev = 0.5;
params.numBest = 1000; %(Number of chips = 26)
bestFits = ellipseDetection(edgeMask, params);
minCenterDistance = 10;
minScore = 30;
maxAspectRatio = 0.6;
bestFits = pareEllipseFits(bestFits, ...
    minCenterDistance, minScore, maxAspectRatio);

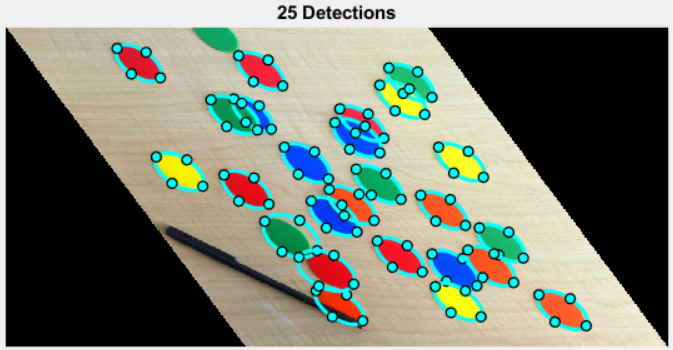
I wrote pareResults to allow filtering by minimum center distance (to disallow overlapping detections), minimum score, and maximum aspect ratio. Using that paring approach, I can request far more detections (params.numBest = 1000) than I really want, then discard "bad" results. I'm pretty pleased with the way it's working!

A Note on Visualizing the Results

Finally, I also wrote visualizeEllipses to call drawellipse directly on the output of ellipseDetection.

Notes

In the interest of making this post a bit shorter (I know...too late!), I didn't post all of the code. If anyone would like to see it, I'm happy to share. Just drop me an email at:

char(cumsum([98 17 -11 7 -10 7 7 -4 -47 45 -12 19 -12 15 -8 3 -7 8 -69 53 12 -2]))

Also, there are a few other files on the Exchange that purport to facilitate ellipse detection. Please leave me a comment if you'd like to see those considered those in a subsequent post!

A Couple of Suggestions

Martin's implementation uses Gaussian filtering via fspecial. That syntax is no longer recommended; the newer imgaussfilt is more efficient. Also, the call to fspecial requires an integer argument for the second ('hsize') parameter. (I added a call to round() in my version.) Finally, since getting good results requires tuning a number of parameters, this function is just begging for a code-generating app to front it; that's perhaps a project for another day!

Thank you, Martin...finding this function, and figuring out how to use it, gives me a valuable tool in my image processing arsenal.

As always, I welcome your thoughts and comments.

Get the MATLAB code

Published with MATLAB® R2022a