MatCal
Will's pick this week is MatCal by Bryan.
I'm no archaeologist, but I read a fair number of books that cover the topic. A common point of discussion is the wonder and challenges of radiocarbon dating. You find yourself organic remains from an ancient site. Take it to the lab and calculate the ratio of carbon 14 to carbon 12 in the sample. Compare that ratio to present organic material. Since carbon 14 decays over time and the remains aren't absorbing fresh carbon 14 from the atmosphere, you can estimate how old it is.
This line of reasoning works well enough if you assume that the ratio of carbon 14 in the atmosphere is constant. But while cosmic rays are regularly creating new carbon 14 isotopes in the air, the ratio does fluctuate over time. There are other factors to consider with the net effect being that you need to adjust dating estimates to improve its accuracy.
Bryan's submission provides a simple function to calibrate carbon 14 dating. You provide the uncalibrated dating estimate and range of uncertainty. You tell it which of thirteen calibration models you'd like to use, and it will adjust your findings. Here's a plot produced for a 4,000 year old sample with a 1 sigma uncertainty of 100 years. I used the IntCal20 model, which was developed in 2020 based on tree rings. The old probability distribution (y axis) is compared against the new probability distribution (x axis) with the calibration curve shown on the main figure. The revised estimate of the specimen's age is more likely to be 4,500 years old.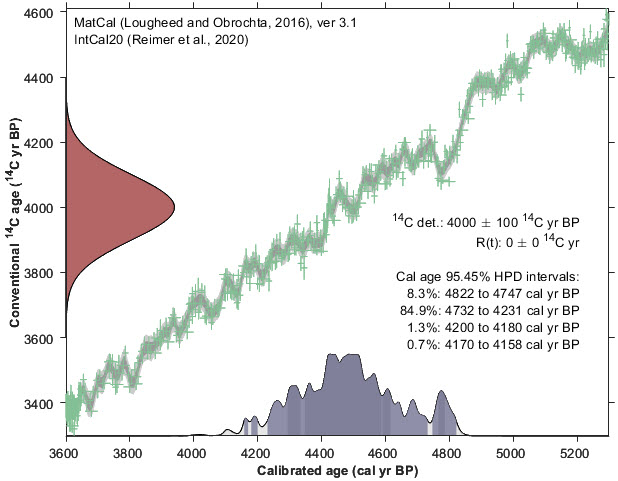
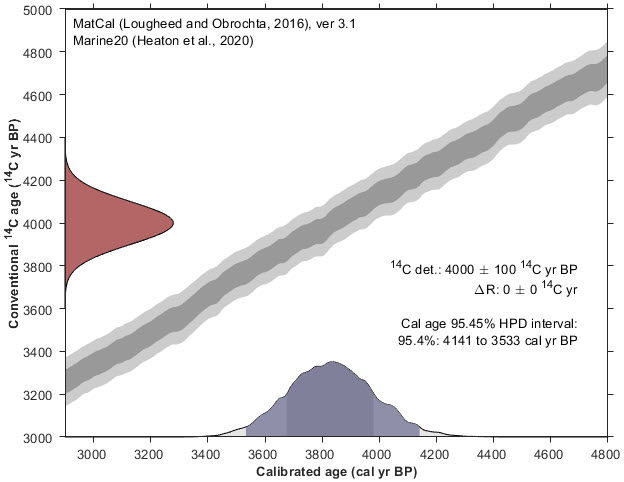
I had read that calibration of marine samples required different considerations. Carbon 14 amounts in the oceans is different than the atmosphere. Nevertheless, I was surprised by how different the results were when I used the Marine20 model. The same input parameters yielded an estimate around 3,800 years, quite a bit younger than with the IntCal20 model.
Bryan's contribution remains popular more than a decade after he initially posted it. I applaud him for continuing to maintain things. His most recent update was made in 2021. For the next iteration, I suggest taking a look at function argument validation. I see your comment on line 126, and I think this might help you out!
Let us know what you think here or leave a comment for Bryan.
I'm no archaeologist, but I read a fair number of books that cover the topic. A common point of discussion is the wonder and challenges of radiocarbon dating. You find yourself organic remains from an ancient site. Take it to the lab and calculate the ratio of carbon 14 to carbon 12 in the sample. Compare that ratio to present organic material. Since carbon 14 decays over time and the remains aren't absorbing fresh carbon 14 from the atmosphere, you can estimate how old it is.
This line of reasoning works well enough if you assume that the ratio of carbon 14 in the atmosphere is constant. But while cosmic rays are regularly creating new carbon 14 isotopes in the air, the ratio does fluctuate over time. There are other factors to consider with the net effect being that you need to adjust dating estimates to improve its accuracy.
Bryan's submission provides a simple function to calibrate carbon 14 dating. You provide the uncalibrated dating estimate and range of uncertainty. You tell it which of thirteen calibration models you'd like to use, and it will adjust your findings. Here's a plot produced for a 4,000 year old sample with a 1 sigma uncertainty of 100 years. I used the IntCal20 model, which was developed in 2020 based on tree rings. The old probability distribution (y axis) is compared against the new probability distribution (x axis) with the calibration curve shown on the main figure. The revised estimate of the specimen's age is more likely to be 4,500 years old.

I had read that calibration of marine samples required different considerations. Carbon 14 amounts in the oceans is different than the atmosphere. Nevertheless, I was surprised by how different the results were when I used the Marine20 model. The same input parameters yielded an estimate around 3,800 years, quite a bit younger than with the IntCal20 model.

Bryan's contribution remains popular more than a decade after he initially posted it. I applaud him for continuing to maintain things. His most recent update was made in 2021. For the next iteration, I suggest taking a look at function argument validation. I see your comment on line 126, and I think this might help you out!
Let us know what you think here or leave a comment for Bryan.
- Category:
- Picks







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.