Round, With Tie Breakers, Round Two
I published Round, With Ties to Even a couple of days ago. Steve Eddins and Daniel Dolan immediately had substantive comments. Here is my reaction to their comments.
Contents
Two More
The four choices that I described for how to break ties -- 'even', 'odd', 'up' and 'down' -- all have the same behavior for positive and negative numbers. The current built-in round uses the 'up" rule.
Steve sees the need for two more choices that are sensitive to the sign of the number. I will call them 'plus' and 'minus". They round to the right and to the left on the number line. That's sometimes known as round toward plus infinity and toward minus infinity.
Sample
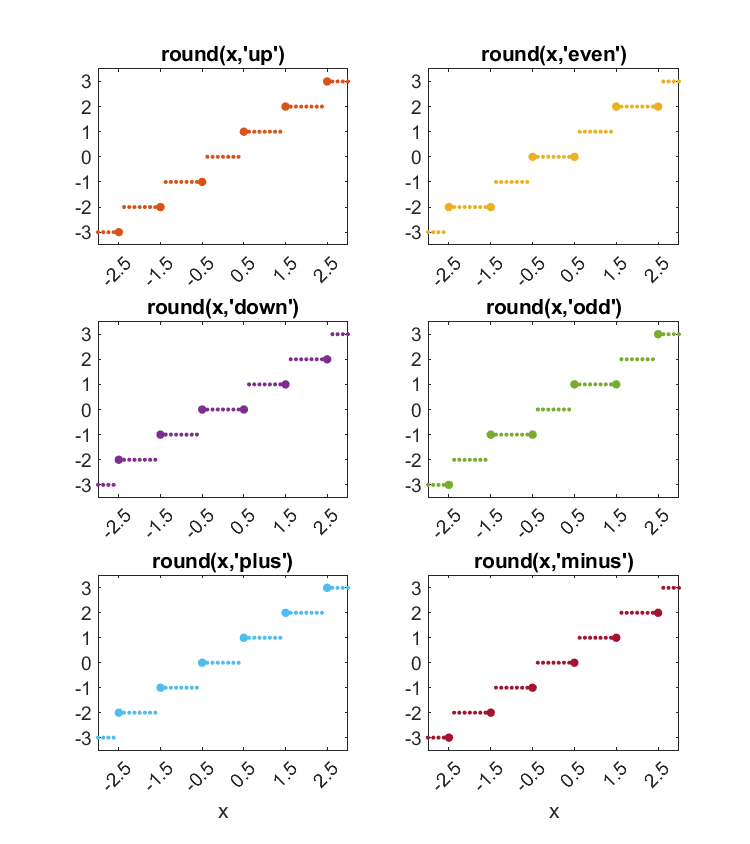
Here's a chart of a few values.
x = (-4.5:1:4.5)';
xRound(x);
x round up down even odd plus minus
-4.500 -5 -5 -4 -4 -5 -4 -5
-3.500 -4 -4 -3 -4 -3 -3 -4
-2.500 -3 -3 -2 -2 -3 -2 -3
-1.500 -2 -2 -1 -2 -1 -1 -2
-0.500 -1 -1 -0 -0 -1 -0 -1
0.500 1 1 0 0 1 1 0
1.500 2 2 1 2 1 2 1
2.500 3 3 2 2 3 3 2
3.500 4 4 3 4 3 4 3
4.500 5 5 4 4 5 5 4
And the plot.
Scaling
The current built-in round also includes the possibility of scaling by a power of 10 to facilitate rounding to, say, the nearest multiple of 1000, or of 1/1000, or three significant figures. Daniel was concerned that having both scaling and tie-breaking options in the same function would be confusing.
But, I think it is OK, because:
- round(x,'even'), the parameter 'even' is a char.
- round(x,3), the parameter 3 is numeric.
- round(x,3,'significant'), the parameter 'significant' is a specific char.
So, the statements
- round(x,'even',3)
- round(x,3,'even')
- round(x,'even',3,'significant')
are unambiguous and distinguishable. After x, the other parameters can be given in any order.
round
Here is my proposal for the enhancement request about round. It is available here.
type round.m
function r = round(varargin)
% r = round(x) scales and rounds the elements of x to the nearest integers.
% Default: ties, elements halfway between integers, are rounded away from zero.
%
% r = round(x,'even') ties round to even integers.
% r = round(x,'odd') ties round to odd integers.
% r = round(x,'up') ties round away from zero (same as default).
% r = round(x,'down') ties round towards zero.
% r = round(x,'plus') ties round to the right on the number line.
% r = round(x,'minus') ties round to the left on the number line.
%
% r = round(x,n), n >= 0, round(10^n*x)/10^n, round(12.3456,2) = 12.3500
% r = round(x,-n), n > 0, 10^n*round(x/10^n), round(1234.56,-2) = 1200.
% r = round(x,n,'significant'), round(.001234,2,'significant') = .0012
% r = round(x,n,'decimals) same as round(x,n).
%
% r = round(x,...), ties, n, 'significant' and 'decimals' can be in any order.
%
% Use Round(...) with capital R to distinguish from built-in round(...).
[x,n,ties] = parse_input(varargin{:});
x = prescale(x,n);
a = abs(x) + 0.5;
r = floor(a);
switch ties
case 'even'
m = (r == a) & (mod(r,2) == 1);
case 'odd'
m = (r == a) & (mod(r,2) == 0);
case 'down'
m = (r == a);
case 'up'
m = [];
case 'plus'
m = (x < 0) & (r == a);
case 'minus'
m = (x > 0) & (r == a);
otherwise
error(['''' ties ''' not recognized.'])
end
r(m) = r(m) - 1;
r = sign(x).*r;
r = postscale(r,n);
% ----------------------------------------------
function [x,n,ties] = parse_input(varargin)
x = varargin{1};
n = zeros(size(x));
ties = 'up';
for k = 2:nargin
if isnumeric(varargin{k})
n(:) = varargin{k};
elseif strcmp(varargin{k},'significant')
n(:) = n(:) - ceil(log10(abs(x(:))));
elseif strcmp(varargin{k},'decimals')
% ignore
else
ties = varargin{k};
end
end
end
function x = prescale(x,n)
if any(n ~= 0)
k = n > 0;
x(k) = 10.^n(k).*x(k);
k = n < 0;
x(k) = x(k)./10.^(-n(k));
end
end
function r = postscale(r,n)
if any(n ~= 0)
k = n > 0;
r(k) = r(k)./10.^n(k);
k = n < 0;
r(k) = 10.^(-n(k)).*r(k);
end
end
end
- Category:
- Numerical Analysis,
- Precision,
- Programming
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building






Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.