Digital Simulation of Rubik’s Cube
Rubik's Cube is one of the great mathematical puzzles of all time. Most people are just interested in solving Rubik's Cube rapidly, but deeper investigation reveals a rich mathematical and computational structure. A digital Rubik's Cube simulator provides a laboratory for the study of linear algebra, group theory, data structures and computer graphics.
Contents
Cubelets
Our abstract Rubik's Cube is made from 27 identical copies of a small cube that I call a cubelet. In the first view below you see three of the traditional colors for the cubelet faces -- green, white and orange. Rotating the cubelet, you see that the face opposite the white face is yellow and the face opposite orange face is red. Rotation about a different axis would reveal that the face opposite the green face is blue.
cubelet
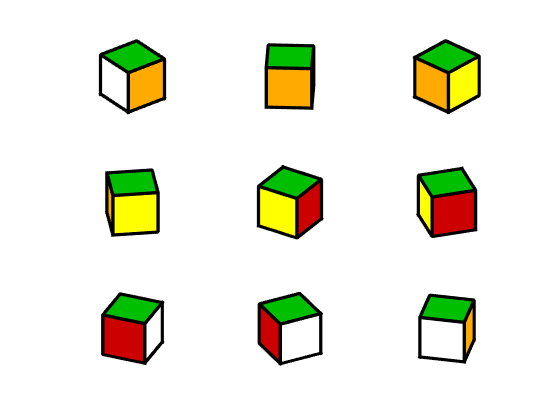
Four types
An ingenious spring mechanism holds an actual physical Rubik's Cube together while allowing rotation of its faces. On the other hand, our computer model of the puzzle does not involve any springs and its faces are rotated by 3-by-3 matrices.
The 27 cubelets in the model have four types -- center, face, edge and corner. The center cubelet is never visible and rotates only when the viewpoint of the entire puzzle is rotated.
There are six cubelets at the centers of the six puzzle faces. They rotate when the corresponding puzzle face is rotated.
There are twelve cubelets in the middle of the twelve puzzle edges. Each edge cubelet shows two colors from its associated faces, green-white, white-orange and so on. There is no orange-red edge cube because the orange and red faces of the puzzle never share a common edge.
There are eight corner cubelets, each showing three colors, green-white-orange, green-orange-yellow, and so on. Of the 6x5x4 = 120 possible combinations of six colors, only eight are needed for the corner cubes.
Here is what would happen if you start with the center plus the six face cubelets, then add the twelve edge cubelets, and finally add the eight corner cubelets.
show_types

Q0
I will use capital letters Q to denote cubes. A cube is a 3-by-3-by-3 cell array. Each cell contains the vertices of a cubelet, stored in an 8-by-3 matrix of doubles. That's a total of 27 vertex matrices, each ready to be multiplied a rotation. Applying the same rotation to all 27 cubelets in a cube rotates the entire cube. It's more interesting to apply a given rotation to the 9 cubelets in one of the cube faces, while leaving the other 18 cubelets unchanged.
I will use Q0 to denote the puzzle that has all the cubelets in a face showing the same color.
Qfigure
Qshow(Q0)

Code
The code for generating Q0 begins with a matrix v containing the vertices of the center cubelet, qzero.
type qzero
function q0 = qzero
% Unit cubelet.
q0 = [-1 -1 -1
-1 -1 1
-1 1 -1
-1 1 1
1 -1 -1
1 -1 1
1 1 -1
1 1 1];
end
With loop variables x, y and z that take on all possible combinations of -2, 0 and +2, the innermost statement involves the quantity
v + [x y z]
This is the sum of a matrix and a vector, which is not defined in conventional linear algebra. MATLAB singleton expansion rewrites this as the sum of two matrices. So, x, y and z are the coordinates of cubelet centers, and the output cell array has the vertices of all the cubelets in Q0.
type Q0.m
function Q = Q0(w)
if nargin < 1
w = width;
end
v = w*qzero;
Q = cell(3,3,3);
for z = [-2 0 2]
for y = [-2 0 2]
for x = [-2 0 2]
Q{x/2+2,y/2+2,z/2+2} = v + [x y z];
end
end
end
end
David Singmaster
David Singmaster was one of the first mathematicians to investigate the Rubik's Cube and his notation for describing moves has become standard. It just so happens that Singmaster was a friend of mine when both of us were undergrads at Caltech in the late 1950's. He subsequently went to grad school at U. C. Berkeley and shortly thereafter moved to England. He has been a math professor ever since at what is now called London South Bank University. Here is a 2018 video interview with Singmaster.
Singmaster uses the letters L, R, U, D, F and R to denote clockwise rotation of the Left, Rear, Up, Down, Front and Back faces. And, one of these letters followed by a ' symbol denotes counterclockwise rotation.
L,U animation
For example, here is an animation of L rotating the "left" face of Q0 clockwise, followed by U rotating the "up" face.

F, F animation
And here is F rotating the "front" face twice.

Z, X' animation
Singmaster's notation also uses X, Y and Z to denote rotation of the entire cube. Here is Z followed by X', revealing the other three traditional colors, red, white and blue.

 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.