Exploring Matrices
I have spent much of my career working to bring abstract linear algebra and practical matrix computation closer together. This project is my latest effort.
Contents
Alibi
Over sixty years ago, as a sophomore contemplating a major in mathematics, I took a course entitled Survey of Modern Algebra. We used a now-classic textbook by MacLane and Birkhoff that featured abstract theorems about groups, rings, fields, vector spaces and linear algebra. I remember the colorful terms alias and alibi had something to do with change of basis and change of position, but I have never seen those terms again.
The next year, I took Numerical Analysis. We did some of the homework on a Burroughs 205 Datatron and I wrote a machine language program to solve simultaneous linear equations. I was hooked.
But at the time I did not realize that the two courses were about the same magnificent object -- the matrix.
Exploring Matrices
Exploring Matrices is a multi-media project that shows matrices in action. Short videos, blog posts, interactive MATLAB software and self-study exercises investigate applications of matrices. The material is intended for students in an undergraduate course in linear algebra or computational science. However, anyone using matrices should find topics that interest them.
The first release of Exploring Matrices has six modules. All of the modules feature animated MATLAB displays and four of the modules include interactive MATLAB "apps". The modules are:
- Matrix Multiplication
- Rotation and Scaling
- Computer Graphics
- Matrices and Cubes
- Simulink
- AI and Gorillas
YouTube Videos
An introduction and six videos ranging in length from one to six minutes, are available on YouTube at
https://youtube.com/playlist?list=PLn8PRpmsu08oGNmtBfFOmgVC0TlXDaLDJ.
The first four of these videos feature animations produced by our four MATLAB apps -- Multiply, Rotate, Grafix, and Qube. The other two videos describe two applications, simulation of control systems and neural networks for facial recognition (of gorillas).
Matrix Multiplication
Some viewers may just be learning the mechanics of matrix multiplication. Other viewers will have encountered it years ago. The traditional algorithm for computing the product of two matrices involves inner products between the rows of the first matrix and the columns of the second. A less familiar algorithm, which involves linear combinations of the columns of the first matrix, is often more efficient and informative. The two approaches produce the same final result from intermediate terms in different orders.
Here is one frame from the animation of these two algorithms generated by our Multiply app. The highlighted element in the first matrix either moves across the rows or goes down the columns.
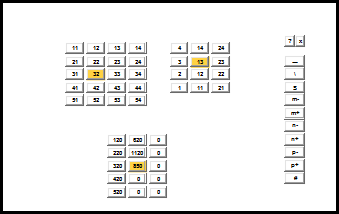
Rotation and Scaling
Our first matrices are 2-by-2. We see how the matrix
$$ R \ = \ \left( \begin{array}{rr} \cos{\theta} & \sin{\theta} \\ -\sin{\theta} & \cos{\theta} \end{array} \right) $$
rotates points by the angle $\theta$, measured in degrees.
We also see how the matrix
$$ S \ = \ \left( \begin{array}{rr} \sigma & 0 \\ 0 & \sigma \end{array} \right) \ \ \ \ \ \ \ \ $$
makes objects larger and smaller.
The two can be combined with matrix multiplication. For more operations in higher dimensions, matrix multiplication provides a unifying framework.
Here is one frame from the animation of rotation and scaling generated by the Rotate app. The first panel displays a 2-by-2 rotation matrix, the second panel displays a 2-by-2 diagonal scaling matrix, and the third panel displays their product.

Computer Graphics
Operations with the 4-by-4 matrices that are at the heart of modern computer graphics employ a system known as "homogeneous coordinates". The leading 3-by-3 submatrix produces rotation and scaling in three dimensions. The fourth column produces translations.
Here is one frame from an animation of rotation about the x-axis generated by the Grafix app. This is often called "pitch". Rotation about the y- and z-axes are "roll" and "yaw",

Matrices and Cubes
Rubik's Cube, named for its inventor, Ernő Rubik, a Hungarian professor of architecture, is the greatest mathematical puzzle of all time. Our digital simulation of the puzzle, Qube, is powered by rotation matrices.
The model consists of 27 identical copies of a single small cubelet whose sides are colored red, white, blue, yellow, orange and green. Initially, all cubelets have the same orientation. A move is the simultaneous rotation of the nine cubelets in one of the six faces, by 90° or 180°, clockwise or counterclockwise. This leads to $4.3 \times 10^{19}$ possible configurations for a scrambled cube.
The object of the puzzle is to return a scrambled cube to the initial state. Most people are interested in solving the puzzle rapidly, but I am more interested in the number of moves required.
Qube offers animations of many mathematical properties of Rubik's cubes. Here is a frame from one of them.

Simulink
MATLAB's companion product, Simulink, is a block diagram programming environment used to design and simulate systems with multidomain models and to automatically generate the code required to operate embedded processors.
Matrices are involved in dozens of different ways by Simulink, but most users rarely see operations at that detailed level. Our Simulink module shows a model of an automobile being driven on a test track and displays the pitch, roll and yaw recorded by the matrix connecting the coordinate system for the automobile to the coordinate system for the track.

AI and Gorillas
This is a personal story about a project in the early stages of development.
My wife and I first visited gorillas in the Volcano National Park of Rwanda twelve years ago. An American primatologist named Dian Fossey had studied the gorillas between 1966 and her murder by poachers in 1985. Her book Gorillas in the Mist was very popular and was the basis for a critically acclaimed 1988 Hollywood movie starring Sigourney Weaver.
We have become good friends with the people in the Gorilla Doctors organization. These African and American veterinarians attend to the health of the roughly 1,000 gorillas in the park. Most of the gorillas have African names like "Inkundwa" and "Maisha". We envision a gorilla facial recognition system that is available on cell phones and tablets so that new guides and doctors can learn the names of their patients.
Inception-v3 is a convolutional neural network (CNN) that is widely used for image processing. We have a version of the network pretrained on more than a million images from the ImageNet database. This publicly available system knows nothing about gorillas. We must do additional training using photos of our unique subjects.
This is where matrices are applied. Training a CNN involves determining the values of thousands of weights and coefficients. The digital photos, regarded as vectors, are repeatedly multiplied by circulant matrices where each row is a shifted copy of the other rows. Importantly, a modern CNN also contains some nonlinear layers.
Here is one photo from a small test collection. Indundwa appears to have his own selfie stick.

Software
A self-extracting MATLAB source archive of our four apps is available at
https://blogs.mathworks.com/cleve/files/Apps_mzip.m
Thanks
Thanks to Jackson Kustell, Josh Bethoney and Heather Gorr from MathWorks and Jan Ramer and Mike Cranfield from Gorilla Doctors.
Dedication
We dedicate the Gorillas project to the memory of Mike Cranfield, DVM. Mike was Executive Director of the Mountain Gorillas Veterinary Project in Rwanda from 1999 until 2014. Before Rwanda, he held various positions at the Maryland Zoo in Baltimore.
Three months ago, Mike sent us a disc drive containing over 14,000 photographs of gorillas he had taken in Rwanda. We are now sorting and organizing the photos to provide specialized training of the facial recognition neural net.
A month ago, Mike was hospitalized from an apparent attack of West Nile Virus. He passed away on August 27. Ironically, after years of working safely in the mountain jungles of Central Africa, it is likely that he acquired the virus from a mosquito bite at his family's cabin in Canada.









Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.