A Pedagogical Tool for Fourier Transforms
I recently attended the DSP Workshop sponsored by the IEEE Signal Processing Society. It focues on both signal processing and signal processing education. I spoke to a lot of the attendees. Some of the professors and instructors mentioned how important it is to teach the basics solidly first, before going into more depth. If the students don't get the fundamentals, then going further doesn't help.
Contents
Pedagogical Tool - dftmtx
With that context, I asked how they teach Fourier transforms, especially once they go from the analog domain to the digital. It turns out that most of them were unaware of some of the tools in Signal Processing Toolbox, such as dftmtx.
Here's the help.
h = help('dftmtx');
disp(h(1:744)) DFTMTX Discrete Fourier transform matrix.
DFTMTX(N) is the N-by-N complex matrix of values around
the unit-circle whose inner product with a column vector
of length N yields the discrete Fourier transform of the
vector. If X is a column vector of length N, then
DFTMTX(N)*X yields the same result as FFT(X); however,
FFT(X) is more efficient.
The inverse discrete Fourier transform matrix is
CONJ(DFTMTX(N))/N.
An interesting example is
D = dftmtx(4)
which returns
D = [1 1 1 1
1 -i -1 i
1 -1 1 -1
1 i -1 -i]
which illustrates why no multiplications are necessary for
4-point DFTs.
See also FFT and IFFT.
The help also mentions fft, the discrete Fourier transform, computed with a fast Fourier transform (fft) algorithm. With the information given for dftmtx, let's compare results with those of fft.
More on dftmtx
On further inspection, you may notice that there are comments in the file outlining the calculation. As an aside, the computation is actually done using the function fft in MATLAB.
Here's a brief description of the non-|fft| algorithm. Basically calculate frequencies on the unit circle and multiply by sqrt(-1) (w). Multiply these by integral steps for the number of points in the transform (w*x). And then calculate all the sin and cos terms using exp.
Explicitly, the calculation is:
f = 2*pi/n; % Angular increment. w = (0:f:2*pi-f/2).' * i; % Column. x = 0:n-1; % Row. D = exp(-w*x); % Exponentiation of outer product.
Compare fft and Discrete Transform Matrix Methods
n = 1024; X = eye(n); Xf = fft(X); % fft result f = 2*pi/n; w = (0:f:2*pi-f/2).' * 1i; x = 0:n-1; Xd = exp(-w*x); % matrix representation norm(Xf-Xd)
ans = 1.6769e-011
Do You Have Good Links for Fourier Transform Teaching Material?
If you know of web sites with good material for teaching discrete Fourier transforms, would you please post them here? Thanks.
- Category:
- Education,
- Less Used Functionality
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building


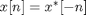




Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.