Solving Ordinary Differential Equations
I have recently handled several help requests for solving differential equations in MATLAB. All of the cases I worked on boil down to how to transform the higher-order equation(s) given to a system of first order equations. In this post I will outline how to accomplish this task and solve the equations in question. What I am not going to talk about is details of ODE solving algorithms (maybe another time).
Contents
Simple System
Let's start with a simple, linear, second order system, a mass-spring system with motion constrained to one-dimension, a horizontal
one (and therefore no gravity). If  is the mass and
is the mass and 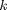 is the spring constant, the equations of motion for the system are:
is the spring constant, the equations of motion for the system are:
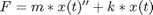
Conditions, Initial and Otherwise
To solve this system, we need to know 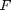 ,
,  ,
, 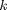 , and initial conditions, e.g.,
, and initial conditions, e.g., 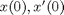 (also known as position and velocity). Let's simplify things and set
(also known as position and velocity). Let's simplify things and set 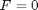 , i.e., no external forces. Let's also set some initial conditions,
, i.e., no external forces. Let's also set some initial conditions, 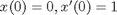 , in other words, start with the spring unstretched and the mass moving. I end up with this system:
, in other words, start with the spring unstretched and the mass moving. I end up with this system:
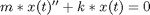
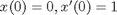
Transform Equation
Looking in the help, I need to set up an system of equations to enable me to use one of the numerical ODE solvers in MATLAB.
To start the transformation, let me define a new variable that I will substitute in the system.
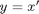
I can derive 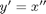
and now rewrite my ODE system in terms of 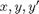 .
.
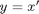
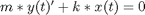
with initial conditions as above.
Now let me reorganize these 2 equations in a vector/matrix equation where 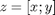
I now write me equation solely in terms of  , the new vector (consisting of position and velocity). With that in mind, I will reorganize the existing equations first
so I have
, the new vector (consisting of position and velocity). With that in mind, I will reorganize the existing equations first
so I have 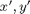 on the left-hand sides.
on the left-hand sides.
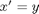
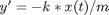
or, in terms of  ,
,
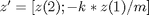
Try It!
Let's try it. Set values for m and k
m = 1; k = 10;
I can create the ODE code in a file, or I can set up the equations as an anonymous function which is what I'll do here.
springmass = @(t,z)[z(2); -k * z(1)/ m];
Set up the initial conditions.
ic = [0; 1];
Solve between 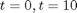 .
.
tspan = [0 10];
Call an ODE solver and plot the results.
[t,y] = ode23(springmass, tspan, ic);
plot(t,y(:,1)), title('Position vs. Time')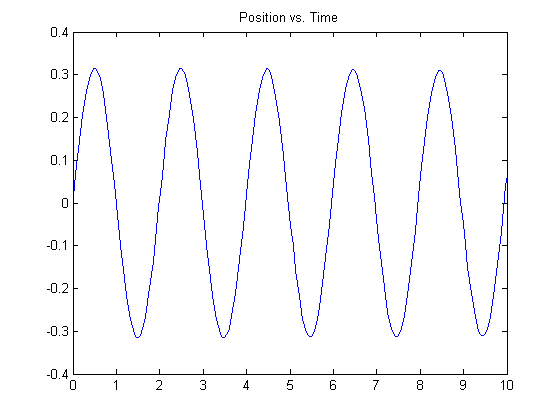
And the velocity.
plot(t,y(:,2)), title('Velocity vs. Time')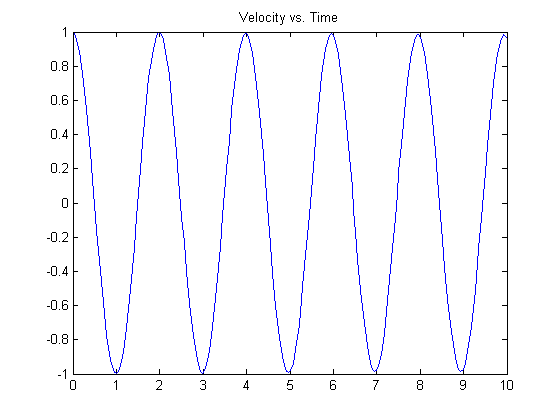
You can see the left-most points on the plots match the initial conditions specified.
Transforming Equations
Do you need to recast problems to fit into a particular formulation such as for solving ODEs? Let's hear about them here.
- Category:
- distance_learning,
- How To
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.