Intersecting Lines
Today I am writing this post in collaboration with my friend and colleague, Lucio Cetto. Ever need to know if two line segments intersect? There are lots of ways to do this, and I thought I would show a few solutions here. I haven't put much thought into how to set up the data so I can vectorize the case for finding out which segments among many intersect and with which ones. At least for now :-)
Contents
Example
Let's start with with some simple line segments. The first column represents to x-values of the line segment, the second column represents the y-values.
line1 = [.5 1; 1 0]; line2 = [.5 0; 1 1];
Plot the data.
h = plot(line1(:,1),line1(:,2)); hold all h(2) = plot(line2(:,1),line2(:,2)); set(h,'linewidth',2) axis([0 1 0 1])

First Algorithm
Using equation y = mx+b, solve for x assuming 2 lines intersect. Then see if that x value is in the necessary range. Special cases: vertical lines (m==inf) and parallel lines (m1 == m2)
First find slopes and intercepts for both line segments. Here are slopes.
slope = @(line) (line(2,2) - line(1,2))/(line(2,1) - line(1,1)); m1 = slope(line1) m2 = slope(line2)
m1 =
-2
m2 =
2
Here are the intercepts.
intercept = @(line,m) line(1,2) - m*line(1,1); b1 = intercept(line1,m1) b2 = intercept(line2,m2) xintersect = (b2-b1)/(m1-m2) yintersect = m1*xintersect + b1
b1 =
2
b2 =
-1
xintersect =
0.75
yintersect =
0.5
Plot results.
plot(xintersect,yintersect,'m*','markersize',8) legend({'line1','line2','intersection'},'Location','West') hold off

Now check that the intersection point is on the line segment and not past the end.
isPointInside = @(xint,myline) ... (xint >= myline(1,1) && xint <= myline(2,1)) || ... (xint >= myline(2,1) && xint <= myline(1,1)); inside = isPointInside(xintersect,line1) && ... isPointInside(xintersect,line2) %
inside =
1
Try with different lines now.
line1 = [.5 1; ... 1 0]; line2 = [.5 0; ... 0 -1];
Compute new intersection.
m1 = slope(line1); m2 = slope(line2); b1 = intercept(line1,m1); b2 = intercept(line2,m2); xintersect = (b2-b1)/(m1-m2) yintersect = m1*xintersect + b1
xintersect =
0.75
yintersect =
0.5
Show the plot.
figure h = plot(line1(:,1),line1(:,2)); hold all h(2) = plot(line2(:,1),line2(:,2)); set(h,'linewidth',2) legend(h,{'line1','line2'},'Location','West') plot(xintersect,yintersect,'g*') hold off axis([-1 1 -1 1])

Is the intersect point on both line segments?
inside = isPointInside(xintersect,line1) && ...
isPointInside(xintersect,line2)inside =
0
No. The intersect point lies on only one line segment, meaning that the two segments don't intersect.
There's still more to think about. What if the two lines segments have the same slope? There are 3 cases for this. First case: the segments are parallel and therefore no intersection. Second and third cases, they are part of the same line, in which case, we have to check to see if they overlap or not (in other words, they may intersect or not, for 2 more cases).
Here are two parallel lines with different values for their y-intercept.
line1 = [.5 1; ... 1 0]; line2 = [.5 3; ... 1 2];
Plot the line segments.
figure h = plot(line1(:,1),line1(:,2)); hold all h(2) = plot(line2(:,1),line2(:,2)); set(h,'linewidth',2) legend(h,{'line1','line2'},'Location','West') hold off

See that slopes are equal, and intercepts are not.
m1 = slope(line1); m2 = slope(line2); b1 = intercept(line1,m1); b2 = intercept(line2,m2); sameSlope = abs(m1-m2) < eps(m1) differentIntercept = abs(b1-b2) > eps(b1) isParallel = sameSlope && differentIntercept
sameSlope =
1
differentIntercept =
1
isParallel =
1
Second Algorithm
Here's another algorithm for seeing if two lines intersect. The idea is to choose one line, and see if the end points from the other line lie on the same side. If they do, there's no way the lines have a point of intersection. If not, the second line might intersect the first one, or the point of intersection may fall outside the limits of the first line segment. A way to test that is to reverse the roles of lines 1 and 2 and do the test again.
The test for checking which side of the line a point falls on is simple. Plug in the values for the end points of line 2 into the equation for line 1. If they are both the same sign, then they both fall on the same side.
line1 = [.5 1; ... 1 0]; line2 = [.5 0; ... 0 -1]; figure h = plot(line1(:,1),line1(:,2)); hold all h(2) = plot(line2(:,1),line2(:,2)); set(h,'linewidth',2) axis([0 1 -1 2])
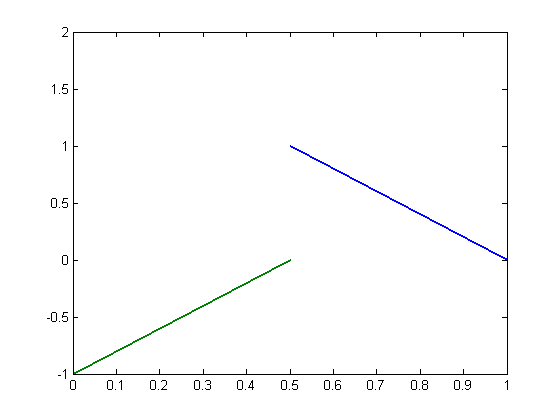
Get slope and intercept of both lines.
m1 = slope(line1) m2 = slope(line2) b1 = intercept(line1,m1) b2 = intercept(line2,m2)
m1 =
-2
m2 =
2
b1 =
2
b2 =
-1
Evaluate the x value of end-points of the second line using the equation y = m*x + b of the first line
lineEq = @(m,b, myline) m * myline(:,1) + b
yEst2 = lineEq(m1, b1, line2)
plot(line2(:,1),yEst2,'om')lineEq =
@(m,b,myline)m*myline(:,1)+b
yEst2 =
1
2

Subtract the end values from the ends of line2 and we find that both values are positive, meaning we don't find that the segment straddles line2.
enderr = @(ends,line) ends - line(:,2) errs1 = enderr(yEst2,line2)
enderr =
@(ends,line)ends-line(:,2)
errs1 =
1
3
Next reverse the roles of lines 1 and 2 and check to see if the end points of line 2 fall on the same side of line 1.
yEst1 = lineEq(m2, b2, line1)
plot(line1(:,1),yEst1,'or')
errs2 = enderr(yEst1,line1)yEst1 =
0
1
errs2 =
-1
1

In this case we find that the differences between the predicted y values and the real y values of line 1 have different signs, which means that if line 2 was long enough there would exist an intersection.
To test for an actual intersection, we now just need to verify that the condition applies in both directions.
possibleIntersection = sum(sign(errs1))==0 && sum(sign(errs2))==0
possibleIntersection =
0
Ignored Issues and Other Algorithms
Here are a list of issues that this post does not solve:
- Vertical line(s) (infinite slope)
Can work around this by rotating the lines to avoid
verticals (try random rotations, or perhaps rotate
through a computed angle so largest angle is bisected
vertically.- Degenerate line (single point)
- Parallel lines with same intercept
- More than two line segments
In addition, there is at least one more algorithm that we haven't talked about here, called Sweep Line Algorithm.
Ever Run Into This Problem Yourself?
How did you solve it? Let us know here.
- Category:
- Computational Geometry,
- How To,
- Puzzles
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.