Simplifying Symbolic Results
I am pleased to introduce guest blogger Kai Gehrs. Kai is a developer for the Symbolic Math Toolbox. His main focus in this post is on special approaches to symbolic simplification and equation solving.
Contents
Have You Noticed Results Not Being Simplified Well?
When using the Symbolic Math Toolbox for symbolic simplification, have you ever been wondering why it does not apply certain classic book rules automatically to return the results you have in mind?
Some of these classic book rules are:
Just using simplify to get the result  on input
on input  does not work:
does not work:
syms a b simplify(log(a)+log(b))
ans = log(a) + log(b)
Using Assumptions on Variables
Of course, we all know that the rule  applies only under appropriate mathematical assumptions on
applies only under appropriate mathematical assumptions on  and
and  . For example, if we assume that
. For example, if we assume that  and
and  are positive, we will get the desired result:
are positive, we will get the desired result:
syms a b positive simplify(log(a)+log(b))
ans = log(a*b)
To get rid of all previously specified assumptions, use
syms a b clear
When Things Get More Complicated
Does it mean that setting the right assumptions is a universal solution here? Well, not always!
Assume  and
and  appear as intermediate results in some really huge symbolic computations somewhere in, lets say, line 454 of your MATLAB
script. From the context of your application, you know that
appear as intermediate results in some really huge symbolic computations somewhere in, lets say, line 454 of your MATLAB
script. From the context of your application, you know that  and
and  are positive. Now you want MATLAB to automatically compute a simplified form of
are positive. Now you want MATLAB to automatically compute a simplified form of  in line 455. How will you manage to set the right assumptions?
in line 455. How will you manage to set the right assumptions?
As an example, think of  and
and  as being something like
as being something like
syms x y a = -(x + 1)^(1/2)/((exp(x - y) - sin(x + y)) * ... (log((x^2 + 1)/(y^2 + 1))/exp(y) + (x - y)^y + ... 1/(x - y)^x)); b = (cos(x)*sin(y))/((x - y)^x*(x + 1)^(1/2)) - ... (exp(x)*(x - y)^y)/(exp(y)*(x + 1)^(1/2)) + ... (cos(y)*sin(x))/((x - y)^x*(x + 1)^(1/2)) - ... (exp(x)*log((x^2 + 1)/(y^2 + 1)))/ ... (exp(2*y)*(x + 1)^(1/2)) - exp(x)/ ... (exp(y)*(x - y)^x*(x + 1)^(1/2)) + ... (cos(x)*sin(y)*(x - y)^y)/(x + 1)^(1/2) + ... (cos(y)*sin(x)*(x - y)^y)/(x + 1)^(1/2) + ... (log((x^2 + 1)/(y^2 + 1))*cos(x)*sin(y))/ ... (exp(y)*(x + 1)^(1/2)) + (log((x^2 + 1)/ ... (y^2 + 1))*cos(y)*sin(x))/(exp(y)*(x + 1)^(1/2));
Now executing the simplify command does not seem to be helpful:
S = simplify(log(a)+log(b)); pretty(S)
/ y
| sin(x + y) sin(x + y) (x - y)
log| ------------------- + ------------------- +
| x 1/2 1/2
\ (x - y) (x + 1) (x + 1)
y
#1 sin(x + y) exp(x) (x - y)
------------- - --------------- -
#2 #2
\
exp(x) #1 exp(x) |
------------------- - -------------------------- | +
1/2 x 1/2 |
exp(2 y) (x + 1) exp(y) (x - y) (x + 1) /
/ 1/2 /
log| - ((x + 1) ) / | (exp(x - y) - sin(x + y))
| |
\ \
/ #1 y 1 \ \ \
| ------ + (x - y) + -------- | | |
| exp(y) x | | |
\ (x - y) / / /
where
/ 2 \
| x + 1 |
#1 = log| ------ |
| 2 |
\ y + 1 /
1/2
#2 = exp(y) (x + 1)
Assuming  and
and  to be positive does not significantly improve the result either. The reason is that we need to set such assumptions on
to be positive does not significantly improve the result either. The reason is that we need to set such assumptions on  and
and  that would make the expressions
that would make the expressions  and
and  positive. We can try to find the right assumptions for this example, but in general it seems like one has to be a genius
to guess what's appropriate.
positive. We can try to find the right assumptions for this example, but in general it seems like one has to be a genius
to guess what's appropriate.
Using Option IgnoreAnalyticConstraints for Simplification
A possible solution to the problem is to ignore certain analytic constraints, that is, to use the IgnoreAnalyticConstraints option for simplify.
With this option the simplifier internally applies the following rules:
 for all values of
for all values of  and
and  . In particular
. In particular  for all values of
for all values of  ,
,  and
and  .
.
 for all values of
for all values of  and
and  . In particular
. In particular  for all values of
for all values of  ,
,  and
and  .
.
- If
 and
and  are standard math functions and
are standard math functions and  holds for all small positive numbers, then
holds for all small positive numbers, then  is assumed to be valid for all
is assumed to be valid for all  (for example as in case of
(for example as in case of  ).
).
So how does this work in our example?
simplify(log(a)+log(b),'IgnoreAnalyticConstraints',true)ans = 0
The result is  , because
, because  . Hence, under the above assumptions, we get
. Hence, under the above assumptions, we get  .
.
Of course, it is important to keep in mind that the rules applied by IgnoreAnalyticConstraints are not correct in a strict mathematical sense. Nevertheless, in practice these rules are often very helpful to get simpler results. Another nice side effect is that ignoring some analytic constraints often helps you speed up your computations.
This documentation describes more details on IgnoreAnalyticConstraints.
Using IgnoreAnalyticConstraints for Equation Solving
Not surprisingly the concept of ignoring analytic constraints also makes sense for equation solving. Imagine that you want
to solve the equation  for
for  . Ignoring analytic constraints would certainly mean to write this as
. Ignoring analytic constraints would certainly mean to write this as  . Assuming
. Assuming  to be nonzero we get
to be nonzero we get  and, finally,
and, finally,  .
.
Without using any restrictions, Symbolic Math Toolbox returns the result:
syms x n solve(log(x^n),x)
Warning: The solutions are parametrized by the symbols: k = Z_ intersect Dom::Interval([-1/(2*Re(1/n))], 1/(2*Re(1/n))) ans = 1/exp((pi*k*2*i)/n)
So you get a parameterized solution which strongly depends on the values of  . This is reasonable, because, for example, for
. This is reasonable, because, for example, for  you get the four solutions
you get the four solutions
solve(log(x^4),x)
ans = 1 -1 i -i
whereas for  there only is one solution:
there only is one solution:
solve(log(x^(1/2)),x)
ans = 1
Applying IgnoreAnalyticConstraints we get
solve(log(x^n),x,'IgnoreAnalyticConstraints',true)ans = 1
Also for equations involving roots where no additional symbolic parameters are present, it may be useful to apply IgnoreAnalyticConstraints to get simpler results:
solve(x^(5/2) - 8^(sym(10/3)), 'IgnoreAnalyticConstraints', true)ans = 16
Here the solver ignores branch cuts during internal simplifications and, hence, returns only one solution.
See the MATLAB doc page on solve for further details.
The IgnoreAnalyticConstraints option can also be used for other Symbolic Math Toolbox functions like the function int for doing symbolic integration. The option is also available for the related MuPAD Notebook Interface functions.
Have You Tried IgnoreAnalyticConstraints?
Have you tried the IgnoreAnalyticConstraints option to get simpler, shorter, and easier to handle results?
Let me know here.
- Category:
- Symbolic
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building
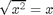








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.