Chaos theory has found uses across a broad set of scientific fields to explain some complicated observed behavior. In geophysics, my background, it can help explain the reversals of Earth's magnetic field, for example. Today I thought I'd share a chaotic system, called Gingerbreadman maps, whose equations make the system seem simple. That is, until you do some simulations.
Contents
Gingerbreadman Map Equations
The equations for the gingerbreadman map look simple enough. For any given point in space: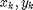 
, define the next point in the sequence by 
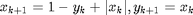. I now show the same equations in this MATLAB code, accounting for some initial values x0,y0 to seed the calculation.
dbtype 17:25 gingerbreadman
17 18 % main calculation 19 for i = 1:n 20 if i == 1 21 x(i) = 1 - y0 + abs(x0); 22 y(i) = x0; 23 else 24 x(i) = 1 - y(i-1) + abs(x(i-1)); 25 y(i) = x(i-1);
Plot Results
I want to show several results from different starting values for x0,y0. First I'll set the random number generator seed for repeatable results.
rng(42) gingerbreadman
gingerbreadman
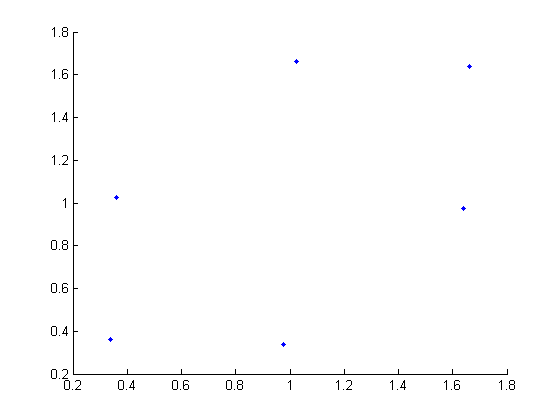
gingerbreadman
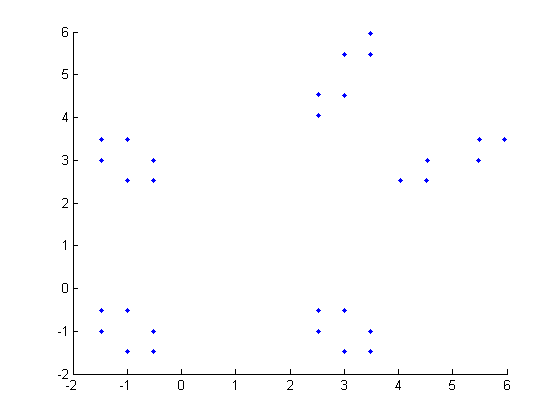
gingerbreadman
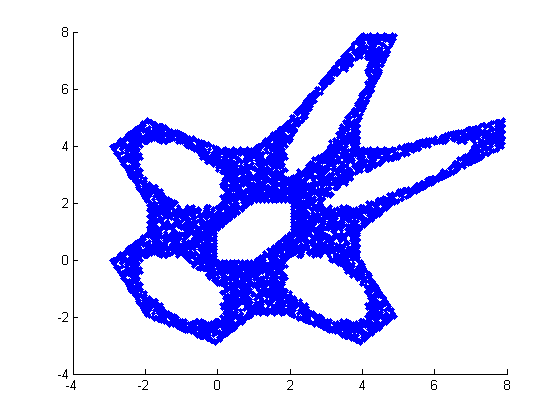
gingerbreadman
Code Listing
Here's the full code listing for gingerbreadman. You can see it allows you to specify the initial conditions, and return points and initial conditions should you choose. With no output arguments, gingerbreadman creates plots like you've been seeing.
type gingerbreadman
function [xout,yout, x0, y0] = gingerbreadman(x0,y0)
% Gingerbreadman map producing a chaotic 2-D map.
% Copyright 2011 The MathWorks, Inc.
% if not enough inputs, assign random numbers
if nargin < 2
x0 = randn();
y0 = randn();
end
% iteration counter
n = 10000;
x = zeros(n,1);
y = zeros(n,1);
% main calculation
for i = 1:n
if i == 1
x(i) = 1 - y0 + abs(x0);
y(i) = x0;
else
x(i) = 1 - y(i-1) + abs(x(i-1));
y(i) = x(i-1);
end
end
% if output is requested, return gingerbread x,y values and
% x0, y0 initial conditions
%
% otherwise plot results
if nargout > 0
xout = x;
yout = y;
else
scatter(x, y, '.');
end
References
Make the Plot Prettier!
Instead of using the plotting function scatter, post your thoughts (in code) here for a chance to win some MATLAB bling. I will look at entries up through (was: Sunday, November 27, 2011) Wednesday December 14, 2011 and announce the winner
(the one whose plot I find most interesting) shortly after that.
Get
the MATLAB code
Published with MATLAB® 7.13
One option to made the plot more meaningful:
(adjust ‘nbins’ to your liking)
nbins = 50;
xbin = linspace(min(x),max(x),nbins);
ybin = linspace(min(y),max(y),nbins);
xbin(end) = xbin(end)+eps(xbin(end));
ybin(end) = ybin(end)+eps(ybin(end));
c = hist3([x,y],’Edges’,{xbin,ybin});
c(c==0) = nan;
figure;
pcolor(xbin,ybin,c);
shading flat
colorbar
You can experiment with different initial conditions and color maps.
%% Housekeeping
close all
clear all
clc
%% Initialize
N=10000;
x=zeros(N,1);
y=zeros(N,1);
%% Initial Conditions
% x(1)=2*rand-1;
% y(1)=2*rand-1;
x(1)=-0.1;
y(1)=0.1;
%% Loop
for n=2:N
x(n)=1-y(n-1)+abs(x(n-1));
y(n)=x(n-1);
end
%% Plot
figure
plot(x,y,’.')
hold on
plot(x(1),y(1),’ro’)
axis equal
grid on
xlabel(‘x’)
ylabel(‘y’)
axis([-4 8 -4 8])
%% Plot 2
numPoints=128;
colorList=jet(numPoints);
figure
hAgedPlot=plot(x(1),y(1),’Marker’,’.’,'LineStyle’,'none’,'Color’,…
colorList(1,:));
hold on
hNewPlot=zeros(numPoints,1);
for n=1:numPoints
hNewPlot(n)=plot(x(1),y(1),’Marker’,’.’,'Color’,colorList(n,:),…
‘MarkerSize’,12);
end
set(gca,’Color’,'none’)
set(gcf,’Color’,'k’)
set(gcf,’Position’,[100 100 640 480])
axis([-6 10 -4 8])
set(gca,’Position’,[0 0 1 1])
axis off
for n=1:N
for m=1:numPoints
nn=n-m+1;
brokeEarly=false;
if nn0
set(hAgedPlot,’XData’,x(1:nn),’YData’,y(1:nn))
end
drawnow
end
As Steve Lord pointed out to me, the deadline is in the past! Change that to Dec. 14, 2011. Sorry for the mistake!
–loren
I used tags, but when I copy my code from the web back into MATLAB, the formatting is messed up and it doesn’t work.
(It’s not just “<" , it's also single quotes etc.)
Any advice?
I don’t have a good option for you. I copy and paste the code and then edit it myself. Sorry for the hassle.
–loren
Loren,
Here’s a suggestion for a winter themed version. The function is mostly the same. Only the plotting is different.
Enjoy.
~Jonathan
function [xout,yout, x0, y0] = gingerbreadman(x0,y0)
% Gingerbreadman map producing a chaotic 2-D map.
% Copyright 2011 The MathWorks, Inc.
% if not enough inputs, assign random numbers
if nargin 0
xout = x;
yout = y;
else
layers = 100;
numPerLayer = ceil(n/layers);
colors = winter(layers);
if numel(unique(x)) < numPerLayer
marker = '*-';
else
marker = '*';
end
hold off
for iLayer = 1:layers
if iLayer == layers
plot3(x((iLayer-1)*numPerLayer+1:end), y((iLayer-1)*numPerLayer+1:end), (iLayer-1)*numPerLayer+1:n, marker, 'MarkerEdgeColor', colors(iLayer,:), 'Color', colors(iLayer,:));
else
plot3(x((iLayer-1)*numPerLayer+1:iLayer*numPerLayer), y((iLayer-1)*numPerLayer+1:iLayer*numPerLayer), (iLayer-1)*numPerLayer+1:iLayer*numPerLayer, marker, 'MarkerEdgeColor', colors(iLayer,:), 'Color', colors(iLayer,:));
end
if iLayer == 1
hold on
end
end
if numel(unique(x)) < numPerLayer
view(0, 85)
else
view(0, 90)
end
end
I think part of my code listing was altered/removed in the post above.
Here it is again.
Yes, I had to use ‘& l t ;’ and ‘& g t ;’ (without spaces) for the less than and greater than symbols.
~Jonathan
function [xout,yout, x0, y0] = gingerbreadman(x0,y0)
% Gingerbreadman map producing a chaotic 2-D map.
% Copyright 2011 The MathWorks, Inc.
% if not enough inputs, assign random numbers
if nargin < 2
x0 = randn();
y0 = randn();
end
% iteration counter
n = 10000;
x = zeros(n,1);
y = zeros(n,1);
% main calculation
for i = 1:n
if i == 1
x(i) = 1 – y0 + abs(x0);
y(i) = x0;
else
x(i) = 1 – y(i-1) + abs(x(i-1));
y(i) = x(i-1);
end
end
% if output is requested, return gingerbread x,y values and
% x0, y0 initial conditions
%
% otherwise plot results
if nargout > 0
xout = x;
yout = y;
else
layers = 100;
numPerLayer = ceil(n/layers);
colors = winter(layers);
if numel(unique(x)) < numPerLayer
marker = '*-';
else
marker = '*';
end
hold off
for iLayer = 1:layers
if iLayer == layers
plot3(x((iLayer-1)*numPerLayer+1:end), y((iLayer-1)*numPerLayer+1:end), (iLayer-1)*numPerLayer+1:n, marker, 'MarkerEdgeColor', colors(iLayer,:), 'Color', colors(iLayer,:));
else
plot3(x((iLayer-1)*numPerLayer+1:iLayer*numPerLayer), y((iLayer-1)*numPerLayer+1:iLayer*numPerLayer), (iLayer-1)*numPerLayer+1:iLayer*numPerLayer, marker, 'MarkerEdgeColor', colors(iLayer,:), 'Color', colors(iLayer,:));
end
if iLayer == 1
hold on
end
end
if numel(unique(x)) < numPerLayer
view(0, 85)
else
view(0, 90)
end
end
I posted mine to File Exchange to avoid the reformatting problem.
http://www.mathworks.com/matlabcentral/fileexchange/34116
One thing it would be nice to extract automatically from the plot is some idea of what the boundary looks like. Getting the convex hull is easy, but the edge of a gingerbreadman is certainly non-convex! There are some interesting methods for finding such boundaries, so I’ve gone off the deep end and coded up the so-called ‘swinging arm’ method as a function. Simply pass it the vectors x and y containing the fractal points, a value for the length of the swinging arm, and a number of points required on the boundary. When the swinging arm length is set to infinity, the method returns the convex hull. You have to play with values for the arm length a bit to get a meaningful boundary shape: too small and it returns disconnected polygons; too large and we get the convex hull.
I’m not sure how pretty it is though!
function gingerboundary(xin,yin,l,bpoints)
% FUNCTION GINGERBOUNDARY(XIN,YIN,L,BPOINTS)
% function to implement swinging arm algorithm for finding a footprint of
% the gingerbreadman fractal set. XIN and YIN are vectors of the x and y
% positions of the points in the set. L sets the radius of nearest
% neighbours to scan, and BPOINTS is the number of boundary points.
% sort points by y-coordinate
p = [xin yin];
plot(p(:,1),p(:,2),’b.’);
n = size(p,1);
p = rot90(sortrows(fliplr(p)),2);
x = p(1,:); xold = x + [0 1];
b = x;
% scan loop
for i=1:bpoints
neighbours = p(sqrt(sum((p-repmat(x,n,1)).^2,2)) eps)
neighbours2 = [neighbours2; neighbours(j,:)];
end
end
% find ‘least clockwise’ point
s2 = size(neighbours2,1);
v = neighbours2-repmat(x,s2,1);
a = angle(v(:,1)+1i*v(:,2));
aprev = angle(xold(1)-x(1)+1i*(xold(2)-x(2)));
adiff = mod(a-aprev,2*pi);
% update
xold = x;
candidates = neighbours2(adiff==max(adiff),:);
x = candidates(1,:);
% plotting
%{
hold on
plot(p(:,1),p(:,2),’b.’);
plot(neighbours2(:,1),neighbours2(:,2),’r.’)
plot(b(:,1),b(:,2));
axis(‘square’);
hold off
drawnow
pause(1);
%}
% update boundary
b = [b; x];
end
% plot boundary
hold on;
plot(p(:,1),p(:,2),’b.’);
plot(b(:,1),b(:,2),’r');
axis(‘square’);
end
I haven’t checked all the other submissions, I hope there’s not yet one too close to mine…
With a minor change in the equation using that y(i) equals x(i-1), I simplified the calculation. However, I therefore produce one more value than can be plotted reasonably. Thus, I take the difference between consecutive values as color code.
n = 10000;
x = zeros(n+2,1);
x(1:2)=randn(1,2);
% main calculation
for cnt = 3:n+2
x(cnt) = 1 – x(cnt-2) + abs(x(cnt-1));
end
scatter(x(2:end),x(1:end-1),3,diff(x))
set(gca,’color’,'k’)
If you take x0 = x(2) and y0 = x(1), Loren’s equations come out with the same values (of course shifted by 2 indices).
This function uses a different approach.The function will map x and y data onto 2d array.This 2d array can be seen as an image.The image generated is grayscale.The darker the pixel more times the formula gets near to that value of x and y.This is same as visualizing a strange attractor.The function is a slow because it stores all the value of x and y.
function [x,y,x0,y0]=myGingerbreadManMap2(x0,y0)
%function takes about 3 seconds to complete
if nargin < 2
x0=randn();
y0=randn();
end
numIterate=1000000;
x=zeros(numIterate,1);
y=zeros(numIterate,1);
x(1)=x0;
y(1)=y0;
for n=2:numIterate
x(n)=1-y(n-1)+abs(x(n-1));
y(n)=x(n-1);
end
%find bounding box
maxX=max(x);
maxY=max(y);
minX=min(x);
minY=min(y);
%500×500 matrix as counter
img=zeros(500,500);
xdiff=(maxX-minX)/500;
ydiff=(maxY-minY)/500;
for n=1:numIterate
indx=floor((x(n)-minX)/xdiff);
indy=floor((y(n)-minY)/ydiff);
if (indx>0 && indy>0 && indx < 500 && indy < 500)
img(indx,indy)=img(indx,indy)+1;
end
end
%scale data
maxP=max(img(:));%maximum number of count
img=255*img/maxP;%scale counts in the range of 0 to 255
%diplay
img=uint8(img);
image(linspace(minX,maxX,500),linspace(maxY,minY,500),img);
axis equal
cmap=1-gray(256);
colormap(cmap);
%save image
%imwrite(img,cmap,’gingerbreadman.png’,’png’);
I was interested in which points were plotted last, so my code plots the first 3/4 of the points in white and then two other colors for the remaining 1/4. I also manually put a background around the plot for clarity.
The function takes a single input (no outputs) which determines the number of plots produced in a single figure, so an input of ’2′ produces 4 plots in a 2×2 grid.
function gingerbreadmansheet(N)
hold off
if nargin< 1
N = 1;
end
n = 10000;
for xtran = 0:(N-1)
for ytran = 0:(N-1)
x0 = randn();
y0 = randn();
x = zeros(1,n);
y = zeros(1,n);
for i = 1:n
if i == 1
x(i) = 1 – y0 + abs(x0);
y(i) = x0;
else
x(i) = 1 – y(i-1) + abs(x(i-1));
y(i) = x(i-1);
end
end
x = x+15*xtran;
y = y+15*ytran;
xv = [-2.5 -3.5 -2.5 -2.5 -3.5 -2 0 1 2 4 5.5 4.5 4.5 5.5 8.5 8.5 5.5 4.5 4.5 5.5 4 2 1 0 -2.5]+15*xtran;
yv = [-2.5 0 1 2 4 5.5 4.5 4.5 5.5 8.5 8.5 5.5 4.5 4.5 5.5 4 2 1 0 -2 -3.5 -2.5 -2.5 -3.5 -2.5]+15*ytran;
ss = get(0,’screensize’);
fill(xv,yv,[ 0.5451 0.2706 0.0745]);
hold on
plot(x(1:3*end/4), y(1:3*end/4),’.w’,'LineWidth’,3,’MarkerSize’,20/N^2);
plot(x((3*end/4+1):7*end/8), y((3*end/4+1):7*end/8),’.',’MarkerSize’,20/N^2,’MarkerEdgeColor’,[.95 0 0]);
plot(x(7*end/8+1:end), y(7*end/8+1:end),’.',’MarkerSize’,20/N^2,’MarkerEdgeColor’,[0 .5 0]);
set(gcf,’position’,[.05 .05 .85 .85]*ss(4))
set(gca,’xlim’,[-4 9+15*xtran],’ylim’,[-4 9+15*ytran],’color’,[.5 .5 .5])
end
end
Here is one more submission… I decided to make a pixelated gingerbread man with the output of the chaotic map, using a
lemniscate of Gerono as his green bow tie :)
function pixelatedGBM
rng(42)
[x,y] = gingerbreadman;
%scale and rotate our gingerbread man
r = [x y] * [cosd(135) -sind(135); sind(135) cosd(135)];
minR = min(r); maxR = max(r);
r = (r – repmat(minR,size(r,1),1))./repmat(maxR-minR,size(r,1),1);
r(:,2) = r(:,2).^1.5;
%create a pixel representation of it
N = 25;
b = linspace(0,1,N);
dif = b(2)-b(1);
[xb,yb] = meshgrid(b,b);
C = zeros(N);
x = r(:,1); y = r(:,2);
for i = 1:numel(xb)
C(i) = length(find(x >= xb(i) & x = yb(i) & y < yb(i)+dif));
end
C = reshape(C,size(xb));
%smooth a little for better results
smooth = @(A,L) ((eye(size(A,1)) + L ^ 2 * diff(eye(size(A,1)),2)' * diff(eye(size(A,1)),2) + 2 * L * diff(eye(size(A,1)))' * diff(eye(size(A,1)))) \ A);
D = smooth(smooth(C,0.1)',0.1)';
%let's draw it :)
set(figure,'Position',[0 0 300 400],'Color',[1 1 1])
movegui(gcf,'center')
set(surf(xb,yb,zeros(size(D)),D),'ZData',xb.*0-0.01);
view(2); shading flat; grid off; axis off equal;
colormap([1 1 1; pink(19)])
hold on
t = linspace(0,2*pi,50);
set(fill((sin(t))/9+0.5,(sin(2*t))/18+0.65,[0 .8 0]),'EdgeAlpha',0)
set(fill((sin(t))/30+0.5,(cos(t))/30+0.65,[0 .9 0]),'EdgeAlpha',0)
t = linspace(0,2*pi,5);
set(fill((sin(t))/20+0.5,(cos(t))/20+0.5,[.8 0 0]),'EdgeAlpha',0)
set(fill((sin(t))/20+0.5,(cos(t))/20+0.3,[.8 0 0]),'EdgeAlpha',0)
plot3(r(1:10:end,1),r(1:10:end,2),r(1:10:end,1)*0-0.005,'.','MarkerSize',3,'MarkerEdgeColor',[1 1 1]);
end
Nice, the < were also messed up into tags in my submission…
here is the original code in pastebin:
http://pastebin.com/hGjWYpji