Considering Performance in Object-Oriented MATLAB Code
I’m pleased to have Dave Foti back for a look at objects and performance. Dave manages the group responsible for object-oriented programming features in MATLAB.
I often get questions along the lines of what performance penalty is paid for using objects or how fast will an object-oriented implementation perform compared with some other implementation. As with many performance questions, the answer is that it very much depends on what the program is trying to do and what parts of its work are most performance-intensive. I see many cases where most of the real work is inside methods of an object that do math on ordinary matrices. Such applications won’t really see much difference with or without objects. I also realize that many MATLAB users aren’t nearly as concerned with run-time performance as with how long it takes to write the program. However, for those applications where performance matters and objects might be used in performance critical parts of the application, let’s look at what can we say about how MATLAB works that might be helpful to consider. We’ll also look at what has changed in recent MATLAB versions.
Contents
How objects spend their time
Let’s start with some basics – some of the places where objects spend time and how to minimize it. Objects will spend time in four basic places – object construction, property access, method invocation, and object deletion.
Object Construction
Object construction time is mostly spent copying the default values of properties from the class definition to the object and then calling the object’s constructor function(s). Generally speaking, there isn’t much to consider about default values in terms of performance since the expressions that create the default values are executed once when the class is first used, but then each object is just given a copy of the values from the class. Generally more superclasses will mean more constructor function calls for each object creation so this is a factor to consider in performance critical code.
Property Access
Property access is one of the most important factors in object performance. While changes over the past several releases have made property performance in R2012a more uniform and closer to struct performance, there is still some additional overhead for properties and the potential for aliasing with handle objects means that handle objects don’t get the same level of optimization that structs and value objects get from the MATLAB JIT. The simpler a property can be, the faster it will be. For example, making a property observable by listeners (using SetObservable/GetObservable) will turn off many optimizations and make property access slower. Using a set or get function will turn off most optimizations and also introduce the extra time to call the set or get function which is generally much greater than the time to just access the property. MATLAB doesn’t currently inline functions including set/get functions and so these are always executed as function calls. MATLAB optimizes property reading separately from property writing so it is important not to add a get-function just because the property needs a set-function.
Consider the following class:
type SimpleCylinder
classdef SimpleCylinder
properties
R
Height
end
methods
function V = volume(C)
V = pi .* [C.R].^2 .* [C.Height];
end
end
end
We can measure the time to create 1000 cylinders and compute their volumes:
tic C1 = SimpleCylinder; for k = 1:1000, C1(k).R = 1; C1(k).Height = k; end V = volume(C1); toc
Elapsed time is 0.112309 seconds.
Now consider a slightly different version of the above class where the class checks all the property values:
type SlowCylinder
classdef SlowCylinder
properties
R
Height
end
methods
function V = volume(C)
V = pi .* [C.R].^2 .* [C.Height];
end
function C = set.R(C, R)
checkValue(R);
C.R = R;
end
function C = set.Height(C, Height)
checkValue(Height);
C.Height = Height;
end
end
end
function checkValue(x)
if ~isa(x, 'double') || ~isscalar(x)
error('value must be a scalar double.');
end
end
We can measure the same operations on this class:
tic C2 = SlowCylinder; for k = 1:1000, C2(k).R = 1; C2(k).Height = k; end A = volume(C2); toc
Elapsed time is 0.174094 seconds.
Optimizing for Property Usage Inside the Class
If much of the performance critical code is inside methods of the class, it might make sense to consider using two property definitions for properties accessed in such performance critical code. One property is private to the class and doesn’t define any set or get functions. A second dependent property is public and passes through to the private property but adds error checking in its set-function. This allows the class to check values coming from outside the class, but not check values inside the class. Set functions always execute except when setting the default value during object creation and this allows the class to use its public interface if it is more convenient to do so. Set functions may do convenient transformations or other work in addition to just checking that the input value is legal for the property. However, if a performance-critical method doesn’t need this work, it can be helpful to use two properties.
For example, consider a new version of the cylinder class that checks its inputs but is designed to keep loops inside the class methods and use unchecked properties inside those methods.
type NewCylinder
classdef NewCylinder
properties(Dependent)
R
Height
end
properties(Access=private)
R_
Height_
end
methods
function C = NewCylinder(R, Height)
if nargin > 0
if ~isa(R, 'double') || ~isa(Height, 'double')
error('R and Height must be double.');
end
if ~isequal(size(R), size(Height))
error('Dimensions of R and Height must match.');
end
for k = numel(R):-1:1
C(k).R_ = R(k);
C(k).Height_ = Height(k);
end
end
end
function V = volume(C)
V = pi .* [C.R_].^2 .* [C.Height_];
end
function C = set.R(C, R)
checkValue(R);
C.R_ = R;
end
function R = get.R(C)
R = C.R_;
end
function C = set.Height(C, Height)
checkValue(Height);
C.Height_ = Height;
end
function Height = get.Height(C)
Height = C.Height_;
end
end
end
function checkValue(x)
if ~isa(x, 'double') || ~isscalar(x)
error('value must be a scalar double.');
end
end
Here we measure the same operations as above.
tic C3 = NewCylinder(ones(1,1000), 1:1000); A = volume(C3); toc
Elapsed time is 0.006654 seconds.
Method Invocation
Method invocation using function call notation e.g. f(obj, data) is generally faster than using obj.f(data). Method invocation, like function calls on structs, cells, and function handles will not benefit from JIT optimization of the function call and can be many times slower than function calls on purely numeric arguments. Because of the overhead for calling a method, it is always better to have a loop inside of a method rather than outside of a method. Inside the method, if there is a loop, it will be faster if the loop just does indexing operations on the object and makes calls to functions that are passed numbers and strings from the object rather than method or function calls that take the whole object. If function calls on the object can be factored outside of loops, that will generally improve performance.
Calling a method on an object:
C4 = NewCylinder(10, 20); tic for k = 1:1000 volume(C4); end toc
Elapsed time is 0.013509 seconds.
Calling a method on the object vector:
C5 = NewCylinder(ones(1,1000), 1:1000); tic volume(C5); toc
Elapsed time is 0.001903 seconds.
Calling a function on a similar struct and struct array First calling the function inside a loop:
CS1 = struct('R', 10, 'Height', 20); tic for k = 1:1000 cylinderVolume(CS1); end
Next, we call the function on a struct array:
toc CS2 = struct('R', num2cell(ones(1,1000)), ... 'Height', num2cell(1:1000)); tic cylinderVolume(CS2); toc
Elapsed time is 0.008510 seconds. Elapsed time is 0.000705 seconds.
Deleting Handle Objects
MATLAB automatically deletes handle objects when they are no longer in use. MATLAB doesn't use garbage collection to clean up objects periodically but instead destroys objects when they first become unreachable by any program. This means that MATLAB destructors (the delete method) are called more deterministically than in environments using garbage collection, but it also means that MATLAB has to do more work whenever a program potentially changes the reachability of a handle object. For example, when a variable that contains a handle goes out of scope, MATLAB has to determine whether or not that was the last reference to that variable. This is not as simple as checking a reference count since MATLAB has to account for cycles of objects. Changes in R2011b and R2012a have made this process much faster and more uniform. However, there is one aspect of object destruction that we are still working on and that has to do with recursive destruction. As of R2012a, if a MATLAB object is destroyed, any handle objects referenced by its properties will also be destroyed if no longer reachable and this can in turn lead to destroying objects in properties of those objects and so on. This can lead to very deep recursion for something like a very long linked list. Too much recursion can cause MATLAB to run out of system stack space and crash. To avoid such an issue, you can explicitly destroy elements in a list rather than letting MATLAB discover that the whole list can be destroyed.
Consider a doubly linked list of nodes using this node class:
type dlnode
classdef dlnode < handle
properties
Data
end
properties(SetAccess = private)
Next
Prev
end
methods
function node = dlnode(Data)
node.Data = Data;
end
function delete(node)
disconnect(node);
end
function disconnect(node)
prev = node.Prev;
next = node.Next;
if ~isempty(prev)
prev.Next = next;
end
if ~isempty(next)
next.Prev = prev;
end
node.Next = [];
node.Prev = [];
end
function insertAfter(newNode, nodeBefore)
disconnect(newNode);
newNode.Next = nodeBefore.Next;
newNode.Prev = nodeBefore;
if ~isempty(nodeBefore.Next)
nodeBefore.Next.Prev = newNode;
end
nodeBefore.Next = newNode;
end
function insertBefore(newNode, nodeAfter)
disconnect(newNode);
newNode.Next = nodeAfter;
newNode.Prev = nodeAfter.Prev;
if ~isempty(nodeAfter.Prev)
nodeAfter.Prev.Next = newNode;
end
nodeAfter.Prev = newNode;
end
end
end
Create a list of 1000 elements:
top = dlnode(0); tic for i = 1:1000 insertBefore(dlnode(i), top); top = top.Prev; end toc
Elapsed time is 0.123879 seconds.
Destroy the list explicitly to avoid exhausting the system stack:
tic while ~isempty(top) oldTop = top; top = top.Next; disconnect(oldTop); end toc
Elapsed time is 0.113519 seconds.
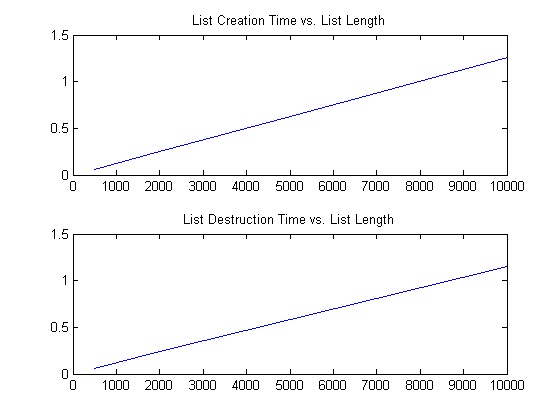
Measure time for varying lengths of lists. We expect to see time vary linearly with the number of nodes.
N = [500 2000 5000 10000]; % Create a list of 10000 elements: CreateTime = []; TearDownTime = []; for n = N top = dlnode(0); tic for i = 1:n insertBefore(dlnode(i), top); top = top.Prev; end CreateTime = [CreateTime;toc]; tic while ~isempty(top) oldTop = top; top = top.Next; disconnect(oldTop); end TearDownTime = [TearDownTime; toc]; end subplot(2,1,1); plot(N, CreateTime); title('List Creation Time vs. List Length'); subplot(2,1,2); plot(N, TearDownTime); title('List Destruction Time vs. List Length');
A Look to the Future
We continue to look for opportunities to improve MATLAB object performance and examples from you are very helpful for learning what changes will make an impact on real applications. If you have examples or scenarios you want us to look at, please let me know. Also, if you have your own ideas or best practices, it would be great to share them as well. You can post ideas and comments here.
- Category:
- Object-oriented
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building






Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.