Traveling Salesman Problem – Genetic Algorithm
Will's picks this week is Traveling Salesman Problem - Genetic Algorithm by Joseph Kirk.
I stumbled upon this submission purely by accident while looking for something completely unrelated. It just goes to show that you never know what goodies you'll discover on the File Exchange. The function converges on the optimal solution to the traveling salesman problem by employing a genetic algorithm. Ok, what does that mean, exactly?
The traveling salesman has a set of cities he or she wishes to visit. The salesman wants to visit each city only once before returning to the city of embarkation. In which order should the salesman visit the cities to minimize the distance traveled? Well, if there are a handful of cities, you could probably figure this out through inspection. But what do you do when there are hundreds of cities to visit?
There are many approaches to solving this problem. In Joseph's case, he opted for a genetic algorithm. He creates a population of possible routes, determines the best route in the population, mutates the best route to get new samples in his population, and repeats the process. He accomplishes all of this with core MATLAB commands. If you're interested in additional capabilities in this arena, check out the Global Optimization Toolbox.
What I like about this submission is its simplicity and ease of use. The code is well-documented such that even a non-expert on the subject (such as me) can readily understand it and make changes as desired. It has a handy option to view the pathway's evolution; with nothing but a simple plot command, Joseph provides us with some strangely addictive animation.
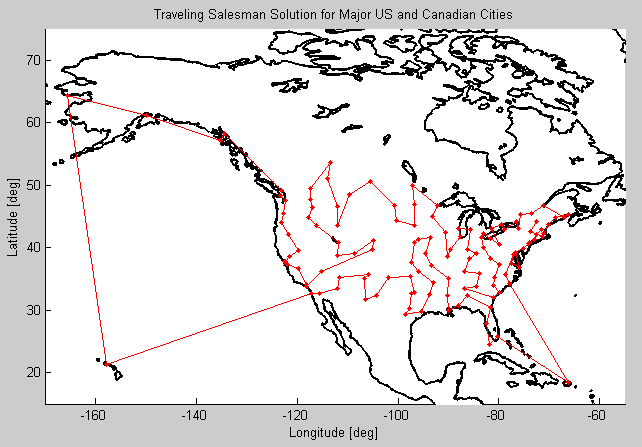
I applied the function to a real-world problem by collecting latitude and longitude values for major US and Canadian cities off the web. I converted the HTML table into an Excel file, imported the data to MATLAB, and used the resultant vector as my input to the Traveling Salesman function. In order to see my results on a map, I added an extra line of code from the Mapping Toolbox:
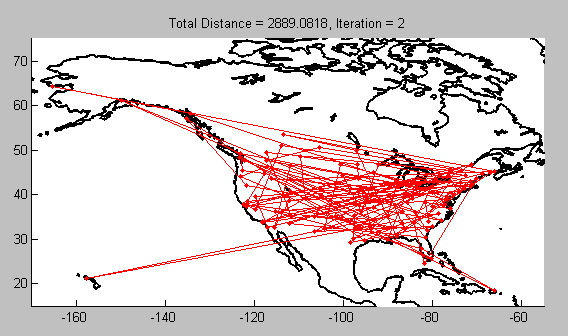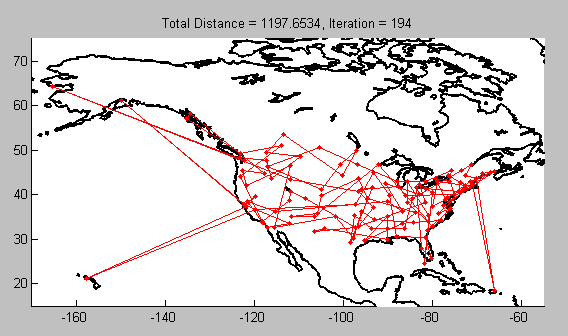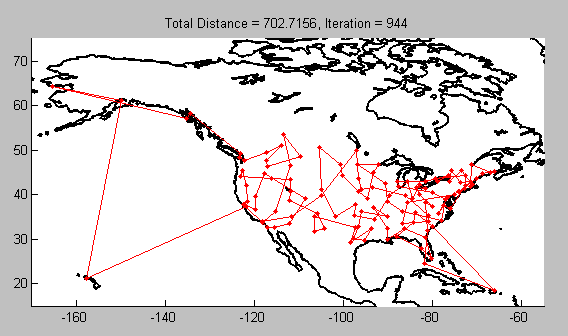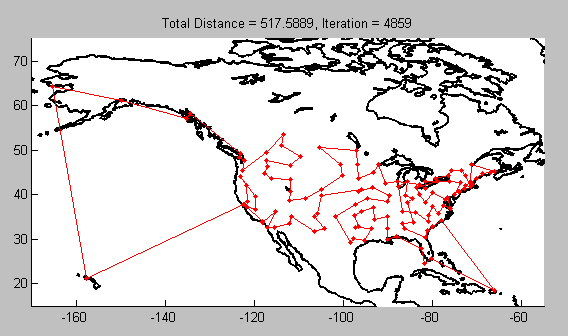
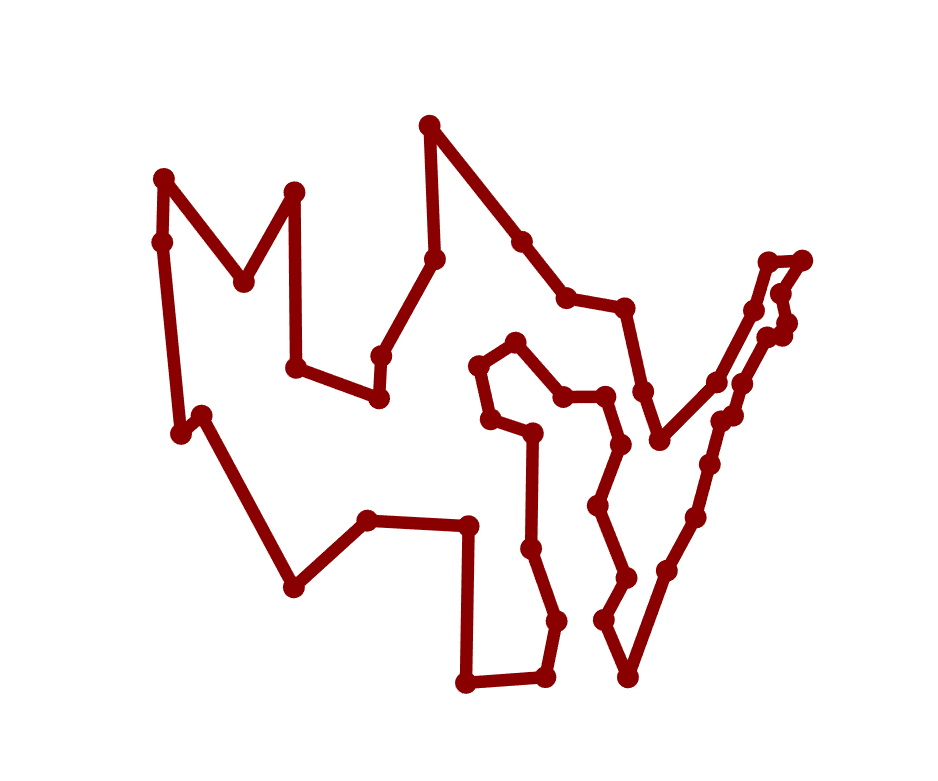
The proposed best route is as follows (different map projection for easier viewing):
Comments
Let us know what you think here or leave a comment for Joseph.
I stumbled upon this submission purely by accident while looking for something completely unrelated. It just goes to show that you never know what goodies you'll discover on the File Exchange. The function converges on the optimal solution to the traveling salesman problem by employing a genetic algorithm. Ok, what does that mean, exactly?
The traveling salesman has a set of cities he or she wishes to visit. The salesman wants to visit each city only once before returning to the city of embarkation. In which order should the salesman visit the cities to minimize the distance traveled? Well, if there are a handful of cities, you could probably figure this out through inspection. But what do you do when there are hundreds of cities to visit?
There are many approaches to solving this problem. In Joseph's case, he opted for a genetic algorithm. He creates a population of possible routes, determines the best route in the population, mutates the best route to get new samples in his population, and repeats the process. He accomplishes all of this with core MATLAB commands. If you're interested in additional capabilities in this arena, check out the Global Optimization Toolbox.
What I like about this submission is its simplicity and ease of use. The code is well-documented such that even a non-expert on the subject (such as me) can readily understand it and make changes as desired. It has a handy option to view the pathway's evolution; with nothing but a simple plot command, Joseph provides us with some strangely addictive animation.
I applied the function to a real-world problem by collecting latitude and longitude values for major US and Canadian cities off the web. I converted the HTML table into an Excel file, imported the data to MATLAB, and used the resultant vector as my input to the Traveling Salesman function. In order to see my results on a map, I added an extra line of code from the Mapping Toolbox:
geoshow( 'landareas.shp', 'FaceColor', 'LineWidth',2);I inserted this line outside the main loop, which required some manipulation of the inner loop, but geoshow is the key command to get the map displayed. In the end, this was the fruit of my labor:

The proposed best route is as follows (different map projection for easier viewing):

Comments
Let us know what you think here or leave a comment for Joseph.
- Category:
- Picks







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.