Solve it, and Solve it Right!
Now for something a little different. As some of you may know, most of the free time that I spend in front of a computer is absorbed by MATLAB Answers. So this week I am going to highlight one of my favorite questions and some of the answers to it.
Sean's pick this week is Seth's Answer to Sven's Question about numerical packing.
Background on The Question (Personal Narrative)
I started working at MathWorks in late November, 2011. When Sven asked this question a few weeks later, my wife had not yet moved to Massachusetts. It was December in my temporary not-so-energy efficient house so I was saving costs by keeping the house at 50F (10C) and staying late at work.
This question came in at the end of the work day and immediately caught my attention. I spent the next five hours coming up with an answer.
A year or so later, Seth, our Optimization Toolbox Product Marketing Manager, was showcasing some new technology to the engineers where he debuted the Sudoku Solver that Alan wrote about a few weeks ago and the solution to the Traveling Sales Man problem. This actually interested me more since it brought back memories of Transportation Engineering classes in college. This new technology was still a few releases away from being ready but the potential was already obvious. I sent Seth this question to see if it would be a good candidate and he replied with the optimal answer in about an hour.
When R2014a was release earlier this Month, he agreed to post his answer.
Background on the Question (Technical)
So what is the question? The goal of the question is to optimally group some elements into bins to minimize both the number of bins and the size of the biggest bin. Each bin has a maximum size and the elements can not be rearranged from their original order. This is a type of optimization problem known as a knapsack problem (thanks Walter!).
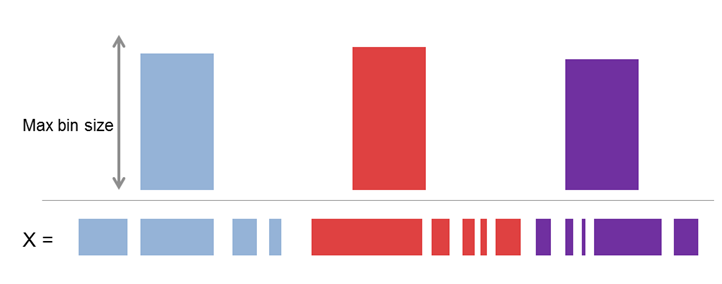
The Runner-Up Answers
The first answer to roll in came from Elige Grant. He posted a way to do this with brute force. For small problems, this will be quick enough and the optimal solution will obviously be found and guaranteed.
As the problem size grows, however, brute force starts to become cumbersome in terms of computational resources. My solution was to use the only solver at the time that we had for mixed integer optimization, ga, the genetic algorithm solver. This solver has an option, 'IntCon', to constrain variables to integers, a requirement. I'd also only been able to have access to the Global Optimization Toolbox for the last few weeks, so this was a chance to play with something new. It did work too (!), for small problems. Once again, as the problem size grew, this approach fell apart and there's no way to prove optimality (or lack thereof) from it.
The Best Answer
Enter intlinprog.
In R2014a we introduced intlinprog, a mixed-integer linear programming solver. This solver will solve any mixed-integer linear programming problem, be it a minimization or a feasibility study. If requested it will also prove that the solution is optimal for a minimization problem.
Let's examine how it's done:
% The call to |intlinprog| looks like this:
[xopt,fval,eflag,output] = intlinprog(f, intIdxs, A, b, Aeq, beq, lb, ub);LP: Optimal objective value is 765.000000.
Cut Generation: Applied 10 implication cuts.
Lower bound is 765.000000.
Heuristics: Found 1 solution using rss.
Upper bound is 939.000000.
Relative gap is 18.50%.
Cut Generation: Applied 2 gomory cuts,
and 7 implication cuts.
Lower bound is 785.000000.
Relative gap is 16.37%.
Branch and Bound:
nodes total num int integer relative
explored time (s) solution fval gap (%)
9 0.01 2 9.220000e+02 1.044609e+01
12 0.01 2 9.220000e+02 0.000000e+00
Optimal solution found.
Intlinprog stopped because the objective value is within a gap tolerance of the
optimal value; options.TolGapAbs = 0 (the default value). The intcon variables
are integer within tolerance, options.TolInteger = 1e-05 (the default value).
- f, objective function coefficients, zeros
- intIdxs, the integer constraints, are the integers between one and 52 meaning every variable is integer constrained
- A, contribution of each element to a bin, and that it must be in a bin greater than or equal to the previous element
- b, is the upper limit on the bin sizes
- Aeq, each element for each of the bins
- beq is all ones, each element is in only one bin
- lb, the lower bound, is all zeros
- ub, the upper bound, is all ones
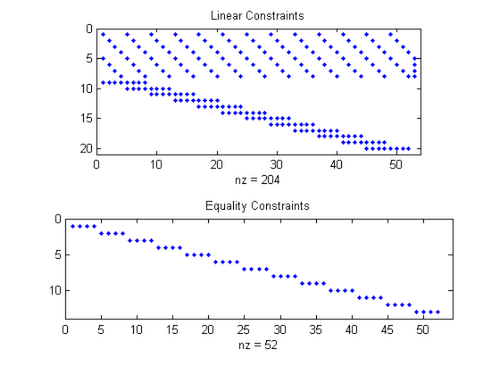
We can see the sparsity patterns of A and Aeq the linear and equality constraints using spy()
subplot(2,1,1) spy(A) title('Linear Constraints') subplot(2,1,2) spy(Aeq) title('Equality Constraints')
Now let's look at output
output
output =
relativegap: 0
absolutegap: 0
numfeaspoints: 2
numnodes: 12
constrviolation: 1.7764e-15
message: 'Optimal solution found.
Since absolutegap is 0, this is the best solution.
If we were curious on time, that took about 0.037s to run!
Comments
Do you have a problem that could be solved with mixed-integer linear programming, or one that you're not sure about and would like our thoughts on? Let us know about it here.
Also, if you liked this post, and you're still reading at this point (which probably biases the data): Would you like me to write another out of model Pick Of The Week post that highlights an intlinprog practical example?
- Category:
- Picks








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.