Perfect Shuffles of Playing Cards
When a deck of playing cards is shuffled perfectly, the result is not random. A perfect shuffle places the cards in a mathematically precise order. As a result, when the most common version of a perfect shuffle is repeated eight times, the deck returns to its original state.
Contents
A Deck of Playing Cards
Fresh out of its package, a deck of playing cards always has the Ace of Spades first, followed by the rest of the spades. The hearts, in order, are next, followed by the clubs (shown here in green), and finally the diamonds (blue). The King of Diamonds is last. Here is a view of a fresh deck.
v = 1:52; deck_view(v) title(0)

Faro Shuffles
A perfect shuffle is also known as a faro shuffle, because it is used frequently in the classic card game, Faro. The deck is cut into two packs, each containing exactly half of the cards. Then the two packs are merged by precisely interleaving the cards.
There are two variants. In an out-faro shuffle, the merger is started with the top card from the first half and eventually completed with the last card from the second half. So with an out-faro shuffle of a fresh deck, the Ace of Spades remains on top and the King of Diamonds remains on the bottom. An in-faro shuffle is started with the second half. So the Ace of Spades and the King of Diamonds are inserted in the second and next to last positions respectively.
Out-Faro
A shuffle is a permutation of the elements of a vector representing the deck. Here is the index vector that produces an out-faro shuffle. A rectangular matrix is created with 1:26 in the first row and 27:52 in the second. So its first column is [1;27], its second column is [2;28], and so on. The reshape operation, which is carried out by columns, then generates the desired index vector.
pout = reshape([1:26; 27:52],[1,52])
pout =
Columns 1 through 13
1 27 2 28 3 29 4 30 5 31 6 32 7
Columns 14 through 26
33 8 34 9 35 10 36 11 37 12 38 13 39
Columns 27 through 39
14 40 15 41 16 42 17 43 18 44 19 45 20
Columns 40 through 52
46 21 47 22 48 23 49 24 50 25 51 26 52
Here is the result of two successive out-faro shuffles of a fresh deck.
v = 1:52; v = v(pout); deck_view(v) title(1)

v = v(pout); deck_view(v) title(2)

The four Aces have moved to the front and the four Kings are bringing up the rear.
It takes only 8 Out-Faro shuffles.
Let's start over with a fresh deck, apply the pout permutation eight times, and capture the results in an animated gif. The deck is returned to its original state in just 8 steps.
v = 1:52; deck_view(v) title(0) for t = 1:8 v = v(pout) deck_view(v) title(t) end
In-Faro
Here is the indexing vector for the in-faro suffle.
pin = reshape([27:52; 1:26],[1,52])
pin =
Columns 1 through 13
27 1 28 2 29 3 30 4 31 5 32 6 33
Columns 14 through 26
7 34 8 35 9 36 10 37 11 38 12 39 13
Columns 27 through 39
40 14 41 15 42 16 43 17 44 18 45 19 46
Columns 40 through 52
20 47 21 48 22 49 23 50 24 51 25 52 26
It takes 52 in-faro shuffles to get back to the original state.

Permutation Matrices
Both of the faro shuffles can be represented by permutation matrices. Can you see how their spy plots differ?
I = eye(52);
close
Pout = I(pout,:);
spy(Pout)
title('Pout')

Pin = I(pin,:);
spy(Pin)
title('Pin')

It turns out that the smallest value of t for which the matrix power P^t is equal to the identity matrix is t = 8 for P = Pout and t = 52 for P = Pin.
Eigenvalues.
All of this is explained by eigenvalues. The matrix Pout has order 52, but only 8 distinct eigenvalues, namely the 8-th roots of unity.
plot(eig(Pout),'o') title('eig(Pout)') axis(1.25*[-1 1 -1 1]) axis('square')

On the other hand, Pin has 52 distinct eigenvalues, the 52-nd roots of unity.
plot(eig(Pin),'o') title('eig(Pin)') axis(1.25*[-1 1 -1 1]) axis('square')

Multiplicities
The eigenvalues of Pout occur with different multiplicites. Can you explain where these counts come from?
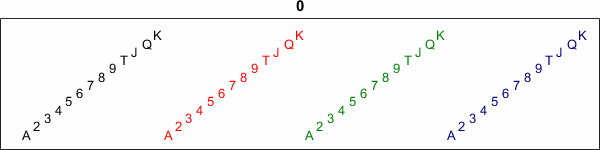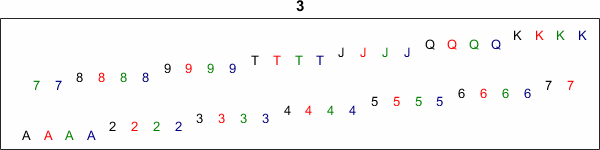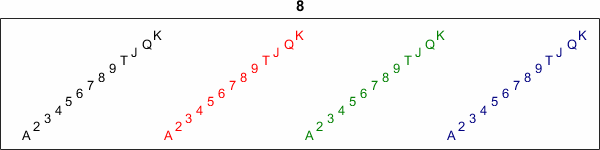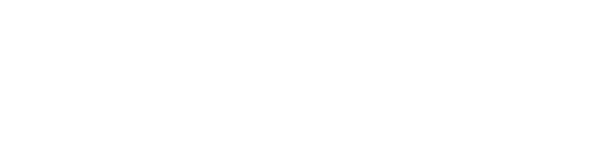
e = eig(Pout); z = exp(pi/4*1i) count = zeros(1,8); for k = 0:7 count(k+1) = sum(abs(e-z^k)<52*eps); end disp(' ') disp('multiplicites = ') disp(' 1 z i z^3 -1 z^5 -i z^7') disp(count)
z =
0.7071 + 0.7071i
multiplicites =
1 z i z^3 -1 z^5 -i z^7
9 6 6 6 7 6 6 6
Deck_view.
Here is the listing of deck_view.
type deck_view
function deck_view(v)
% deck_view(v) displays the card deck v.
% Prepare the figure window.
f = clf;
f.Position = [200 300 600 150];
f.NumberTitle = 'off';
f.ToolBar = 'none';
f.MenuBar = 'none';
f.PaperPositionMode = 'auto';
% Prepare the axes.
ax = axes;
ax.Position = [0 0 1 .88];
ax.XLim = [-1 54];
ax.YLim = [-1 15];
ax.XTick = '';
ax.YTick = '';
ax.Box = 'on';
% Colors for spades, hearts, clubs, diamonds.
shcd = [0 0 0; 1 0 0; 0 .5 0; 0 0 .5];
% Plot one text character per card.
pips = 'A23456789TJQK';
for i = 1:52
j = mod(v(i)-1,13)+1;
k = floor((v(i)-1)/13)+1;
t = text(i,j,pips(j));
t.FontSize = 10;
t.Color = shcd(k,:);
end
end
An informative video.
Kevin Houston is a mathematician at the University of Leeds in the UK who can also do perfect shuffles. Here is a link to his YouTube video. Perfect Shuffle.
- Category:
- Algorithms,
- Eigenvalues,
- Fun,
- Matrices
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.