Loren on the Art of MATLAB

Contents

Tidy up to start.

clear
format short g

Recap the Problem

Sample Input and Results

Supppose array a contains values that we expect to see in another array, Minit.

a = [1 3 5 7 8]
Minit = [1 3 5; ...
    3 5 7; ...
    3 7 8]

a =
     1     3     5     7     8
Minit =
     1     3     5
     3     5     7
     3     7     8

Let's build a replacement matrix for Minit in which its values are replaced with their indices in the list a.

Mwanted = [1 2 3; ...
     2 3 4; ...
     2 4 5]

Mwanted =
     1     2     3
     2     3     4
     2     4     5

Algorithms

We previously compared these algorithms:

Here's loopFR, for reference:

dbtype loopFR

1     function M1 = loopFR(M,A)
2     % loopFR replaces M with its indices from A.
3     
4     % First set up the inverse mapping array.  Initialize it to zero, and the
5     % size is the maximum number the array.  Note that I get away with this
6     % here because all of my numbers in both A and M are positive integers.
7     imap = zeros(1,max(A));  % inverse mapping array
8     % Now fill the inverse map, but placing in the location specified in each
9     % element of A, the index of that element in A.
10    % If A = [1 5 4], then imap = [1 0 0 3 2].
11    imap(A) = 1:length(A);  
12    M1 = M;
13    for k = 1:numel(M)
14        M1(k) = imap(M(k));
15    end

and let's now add the fully vectorized version, vecIM to our comparison.

type vecIM

function M1 = vecIM(M,a) 
%vecIM Inverse mapping. 
imap(a) = 1:length(a);
M1 = imap(M);

Time the New Algorithm and Retime the Former Ones

N = [1 10 100 1000 10000 100000];  % repetitions to test
t = zeros(length(N),4); % set up the timing collection array
for n = 1:length(N)
    % Make a larger matrix to search.
    % loopFR
    M = repmat(Minit,N(n),1);
    tic;
    M1 = loopFR(M,a);
    t(n,1) = toc;
    % ismember
    tic;
    [M2,M2] = ismember(M,a);
    t(n,2) = toc;
    % histc
    tic;
    [M3,M3] = histc(M,a);
    t(n,3) = toc;
    % vecIM
    tic;
    M4 = vecIM(M,a);
    t(n,4) = toc;
    if ~isequal(M1,M2,M3,M4)
        disp('oops')
    end
end

Timing Results

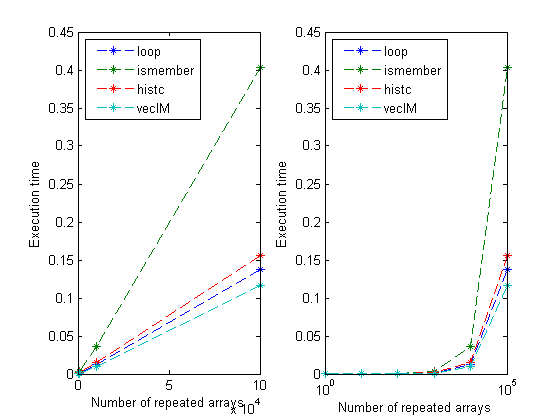
disp('       Counter     loop       ismember     histc        vecIM')
disp([N' t]);
subplot(1,2,1)
plot(N', t, '--*')
xlabel('Number of repeated arrays')
ylabel('Execution time')
legend({'loop','ismember','histc' 'vecIM'},'Location', 'NorthWest')
subplot(1,2,2)
semilogx(N', t, '--*')
xlabel('Number of repeated arrays')
ylabel('Execution time')
legend({'loop','ismember','histc' 'vecIM'},'Location', 'NorthWest')

       Counter     loop       ismember     histc        vecIM
            1  9.0514e-005   0.00028691  2.2349e-005  5.5594e-005
           10  7.2635e-005   0.00024612  3.1568e-005  5.9225e-005
          100   0.00018522   0.00054839   0.00018131   0.00014471
         1000     0.001263    0.0034977    0.0013865   0.00097079
        10000     0.012539     0.035746     0.014809     0.010385
       1e+005      0.13758      0.40348      0.15652      0.11654

Comments

I made a mistake in the original post by not recognizing that loopFR was completely vectorizable. It's often true that if you have the same indexing expression on the right- and left-hand sides, such as on line 14 in loopFR, you can get rid of the loop completely. As you can see, the fully vectorized solution vecIM has the least overhead of all the solutions posted so far. Any more comments, algorithms, or new results? Please add them here.

Published with MATLAB® 7.2