Quick answer: when the result is a NaN.
Contents
NaNs in Arithmetic
MATLAB has followed the IEEE 754: Standard for Binary Floating-Point Arithmetic for doing arithmetic from the early days, and included tools and functionality to achieve similar results on machines that did not comform to the IEEE standards, e.g., Digital Equipment Corporations VAX computers. In addition, we made choices in MATLAB to allow division by 0 rather than causing an error on machine architectures that could handle this behavior (allowed in the IEEE standard). In allowing division by 0, however, we not only encounter cases in which we divide nonzero positive numbers and negative numbers by 0 (yielding Inf and -Inf respectively, but we also encounter computations that result in undefined mathematical outcomes such as
inf-inf
ans = NaN
0/0
Warning: Divide by zero. ans = NaN
NaNs as Placeholders
In addition to allowing NaN as the result of numeric operations, we've also encouraged their use for marking information such as missing data. If we were gathering some data for some specific times, and missed collecting one of the values, we might end up with data that look like this:
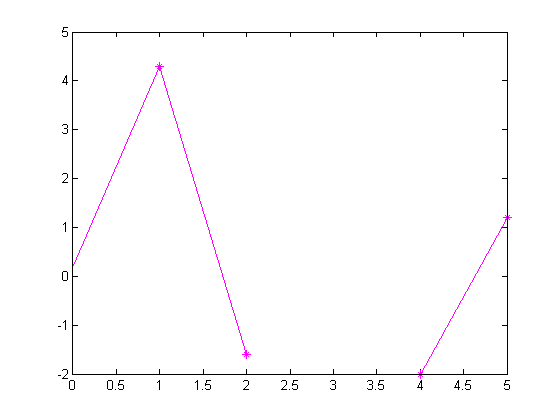
ts = 0:5;
vals = [0.2 4.3 -1.6 NaN -2.0 1.2]
plot(ts,vals,'m*-')vals =
Columns 1 through 5
0.2000 4.3000 -1.6000 NaN -2.0000
Column 6
1.2000
How to Find or Compare to NaN
According to the IEEE standard, NaN is not a number and not equal to anything, including itself. So when looking for NaN values in an array, you can't do the "obvious"
vals == NaN
ans =
0 0 0 0 0 0
As you can see, the comparison is always false. So how do we look for them? Depending on what you are doing, you will find these functions helpful:
Though a mouthful to say or write, isequalwithequalnans allows you to carry out comparisons between arrays matching values and shape, without allowing scalar expansion.
Another way to make look for NaN is frequently cited on the MATLAB newsgroup. See this thread and comments by Paul Bodin for an example. The idea here is that since
NaN == NaN
ans =
0
always produces a false result, we can find NaNs simply by looking for places in which the value doesn't equal itself. These are NaNs, and other values are not.
ourNaNs = vals(vals~=vals)
ourNaNs = NaN
nonNaNs = vals(vals==vals)
nonNaNs =
0.2000 4.3000 -1.6000 -2.0000 1.2000
My preference is to use isnan instead because I find the code much more readable when I revisit it later. However, in some cases, depending on the amount of NaN values (and perhaps other considerations), the constructs just above are sometimes faster. Here are a couple of additional links to newsgroup threads talking more about this.
NaN issues
Some users find themselves experiencing collisions between NaN for missing data vs. NaN as a result of undefined numerical operations.
- Have you encountered such collisions?
- Do you find yourself wishing for more placeholder values?
- What else would you like to use NaN or something similar for?
Let's hear your thoughts.
Published with MATLAB® 7.2
Another handy set of functions for dealing with variables containing NaNs are the nan* descriptive stats functions included in the statistics toolbox: nanmean, nanmedian, nanstd, etc. They save you the trouble of stripping out NaNs when doing simple stats on variables that may have missing data.
Regarding your queries, I seldom run into any missing data vs. undefined NaN collisions, but now that you bring it up, an explicit missing data placeholder would make a lot of sense. It might be helpful to have this placeholder trigger a warning when undefined operations are performed on it, too. For example, I’ll sometimes replace outliers in a timeseries with NaNs for plotting. If I then forget that there are NaNs there and plot a filtfilt’d version of that timeseries, I get nothing if I use an IIR filter, as the NaNs end up propogating throughout. Maybe I’ll eventually just learn to not do that.
Hmm… I am often disturbed by NaNs when evaluating sinc functions or other similar 0/0 cases. Somehow I simply write
>> x = -10:0.1:10
>> y = sin(x)./x
forgetting that Matlab has no way to know that y(x=0)=1.
In case it is not possible to use displaced grid x=[-10:0.1:10]+/-0.05, I typically do
>> x = [-10:0.1:10] + eps
to solve the problem.
Not exactly due to NaN clashes, but in a related subject I would like -1/inf NOT to equal 1/inf. In format hex they are different, but -1/inf == 1/inf returns true.
Perhaps I’m just being picky?
I work with long time series of experimental data from heating and ventilation systems. I wish
to indicate that the data aquisition system was not working
to indicate that the quantity is not defined in the current mode of operation. E.g the inlet air temperature is when the air handling unit it not operating.
I should probably include these two in my Time Series Object.
/ per
I work with long time series of experimental data from heating and ventilation systems. I wish
MissingData to indicate that the data aquisition system was not working
NotDef to indicate that the quantity is not defined in the current mode of operation. E.g the inlet air temperature would be NotDef when the air handling unit it not operating.
I should probably include these two in my Time Series Object.
/ per
Please delete my previous reply. I guess the system swallowed “MissingData” and “NotDef”. / per
Empty matrices, NaN and Inf are great, but fprintf, fscanf, sprintf and sscanf does not handle then consistently. Another inconsistent results are: j*Inf = NaN + j*Inf; Inf+j*Inf = NaN + j*Inf. My workarrounds for both then are complex(0,Inf) and complex(Inf,Inf).
Even though the j doesn’t appear to have a real part, it does — it has a zero real part. That zero real part normally doesn’t make a difference in arithmetic operations, but it does when Inf and/or NaN are involved.
j*Inf = (0+1j)*(Inf+0j)
j*Inf = 0*Inf + 0*0j + 1j*Inf + 1j*0j
j*Inf = NaN + 0j + Inf*1j - 0
j*Inf = NaN + Inf*1j.
The case with Inf+j*Inf is as above, except you add Inf to NaN + Inf*1j to obtain NaN + Inf*1j.
Using COMPLEX as you mentioned is the way to obtain the number with 0 real part and Inf imaginary part, or Inf as both real and imaginary part. Using * does arithmetic; using COMPLEX does not.
Should the result of inf * 0 really be NaN? Why? I have a term a .* (1 - (1 + b .* t) .* exp(-(b .* t))), 0<b0 which should yield a for t=inf. Since b * inf is inf it yields nan. Is this on purpose or a bug?
Gerrit-
Yes, ) * Inf should be 0.
Think about this. Anything times 0 is 0. But inf * anything is infinite. So with 2 answers possible (at least), how to choose? The answer is, don’t - return NaN. MATLAB can’t and doesn’t look at the overall expression you have and calculate limits. If you need special behavior for 0, code that into the algorithm.
–Loren