Comparing Single-threaded vs. Multithreaded Floating Point Calculations
There continue to be a flurry of queries suggesting that MATLAB has bugs when it comes to certain operations like addition with more than values. Sometimes what prompts this is a user noticing that he or she gets different answers when using MATLAB on multiple cores or processors and comparing those results to running on a single core. Here is one example exchange in the MATLAB newsgroup.
In actuality, you can always get different results doing floating point sums in MATLAB, even sticking to a single thread. Most languages do not guarantee an order of execution of instructions for a given line of code, and what you get might be compiler dependent (this is true for C). Having multiple threads simply compounds the issue even more since the compiler has more options for how it will control the statement execution.
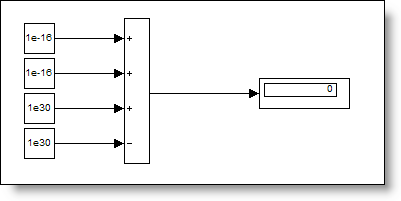
In MATLAB, as you add more elements to a variable, you may see different results depending on how many threads are being used. The reason is numerical roundoff and is not a bug. Fortunately, it is easy to simulate having more than one core or thread for some simple computations by forcing the computational order using parentheses. Let's try out a small example. We'll compute the following expression several ways and compare the results.
1e-16 + 1e-16 + 1e30 - 1e30
Contents
Single Thread (Sequential) Computation
One a single, the sum would get evaluate from left to right. Using parentheses, we can force this to happen.
sequentialSum = ((1e-16 + 1e-16) + 1e30) - 1e30
sequentialSum =
0
Multithreaded Computation (for Two Threads)
The most logical way a vector would get split for between two threads is the first half on one and the second on the other. We simulate that here.
twoThreadSum = (1e-16 + 1e-16) + (1e30 - 1e30)
twoThreadSum =
2e-016
One More Combination
Let's try taking every other element instead. That would essentially be
alternateSum = (1e-16 + 1e30) + (1e-16 - 1e30)
alternateSum =
0
Correctness of Answers
All of the answers are correct! Welcome to the delights of floating point arithmetic. Have you encountered a situation similar to one of these that puzzled you? How did you figure out that the issue was really a non-issue? Do you program defensively when it matters (e.g., don't check for equality for floating point answers, but test that the values lie within some limited range)? Let me know here.
- Category:
- Common Errors,
- Numerical Accuracy
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building






Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.