Measuring GPU Performance
Today I welcome back guest blogger Ben Tordoff who previously wrote here on how to generate a fractal on a GPU. He is going to continue this GPU theme below, looking at how to measure the performance of a GPU.
Contents
Measuring GPU Performance
Whether you are thinking about buying yourself a new beefy GPU or have just splashed-out on one, you may well be asking yourself how fast it is. In this article I will describe and attempt to measure some of the key performance characteristics of a GPU. This should give you some insight into the relative merits of using the GPU over the CPU and also some idea of how different GPUs compare to each other.
There are a vast array of benchmarks to choose from, so I have narrowed this down to three tests.:
- How quickly can we send data to the GPU or read it back again?
- How fast can the GPU kernel read and write data?
- How fast can the GPU do computations?
After measuring each of these, I can compare my GPU with other GPUs.
How Timing Is Measured
In the following sections, each test is repeated many times to allow for other activities going on on my PC and the first-call overheads. I keep the minimum of the results, because external factors can only ever slow down execution.
To get accurate timing figures I use wait(gpu) to ensure the GPU has finished working before stopping the timer. You should not do this in normal code. For best performance you want to let the GPU carry on working whilst the CPU gets on with other things. MATLAB automatically takes care of any synchronisation that is required.
I have put the code into a function so that variables are scoped. This can make a big difference in terms of memory performance since MATLAB is better able to re-use arrays.
function gpu_benchmarking
gpu = gpuDevice();
fprintf('I have a %s GPU.\n', gpu.Name)
I have a Tesla C2075 GPU.
Test Host/GPU Bandwidth
The first test tries to measure how quickly data can be sent-to and read-from the GPU. Since the GPU is plugged into the PCI bus, this largely depends on how good your PCI bus is and how many other things are using it. However, there are also some overheads that are included in the measurements, particularly the function call overhead and the array allocation time. Since these are present in any "real world" use of the GPU it is reasonable to include these.
In the following tests, data is allocated/sent to the GPU using the gpuArray function and allocated/returned to host memory using gather. The arrays are created using uint8 so that each element is a single byte.
Note that PCI express v2, as used in this test, has a theoretical bandwidth of 0.5GB/s per lane. For the 16-lane slots (PCIe2 x16) used by NVIDIA's Tesla cards this gives a theoretical 8GB/s.
sizes = power(2, 12:26); repeats = 10; sendTimes = inf(size(sizes)); gatherTimes = inf(size(sizes)); for ii=1:numel(sizes) data = randi([0 255], sizes(ii), 1, 'uint8'); for rr=1:repeats timer = tic(); gdata = gpuArray(data); wait(gpu); sendTimes(ii) = min(sendTimes(ii), toc(timer)); timer = tic(); data2 = gather(gdata); %#ok<NASGU> gatherTimes(ii) = min(gatherTimes(ii), toc(timer)); end end sendBandwidth = (sizes./sendTimes)/1e9; [maxSendBandwidth,maxSendIdx] = max(sendBandwidth); fprintf('Peak send speed is %g GB/s\n',maxSendBandwidth) gatherBandwidth = (sizes./gatherTimes)/1e9; [maxGatherBandwidth,maxGatherIdx] = max(gatherBandwidth); fprintf('Peak gather speed is %g GB/s\n',max(gatherBandwidth))
Peak send speed is 5.70217 GB/s Peak gather speed is 3.99077 GB/s
On the plot, you can see where the peak was achieved in each case (circled). At small sizes, the bandwidth of the PCI bus is irrelevant since the overheads dominate. At larger sizes the PCI bus is the limiting factor and the curves flatten out. Since the PC and all of the GPUs I have use the same PCI v2, there is little merit in comparing different GPUs. PCI v3 hardware is starting to appear though, so maybe this will become more interesting in future.
hold off semilogx(sizes, sendBandwidth, 'b.-', sizes, gatherBandwidth, 'r.-') hold on semilogx(sizes(maxSendIdx), maxSendBandwidth, 'bo-', 'MarkerSize', 10); semilogx(sizes(maxGatherIdx), maxGatherBandwidth, 'ro-', 'MarkerSize', 10); grid on title('Data Transfer Bandwidth') xlabel('Array size (bytes)') ylabel('Transfer speed (GB/s)') legend('Send','Gather','Location','NorthWest')

Test Memory-Intensive Operations
Many operations you might want to perform do very little computation with each element of an array and are therefore dominated by the time taken to fetch the data from memory or write it back. Functions such as ONES, ZEROS, NAN, TRUE only write their output, whereas functions like TRANSPOSE, TRIL/TRIU both read and write but do no computation. Even simple operators like PLUS, MINUS, MTIMES do so little computation per element that they are bound only by the memory access speed.
I can use a simple PLUS operation to measure how fast my machine can read and write memory. This involves reading each double precision number (i.e., 8 bytes per element of the input), adding one and then writing it out again (i.e., another 8 bytes per element).
sizeOfDouble = 8; readWritesPerElement = 2; memoryTimesGPU = inf(size(sizes)); for ii=1:numel(sizes) numElements = sizes(ii)/sizeOfDouble; data = gpuArray.zeros(numElements, 1, 'double'); for rr=1:repeats timer = tic(); for jj=1:100 data = data + 1; end wait(gpu); memoryTimesGPU(ii) = min(memoryTimesGPU(ii), toc(timer)/100); end end memoryBandwidth = readWritesPerElement*(sizes./memoryTimesGPU)/1e9; [maxBWGPU, maxBWIdxGPU] = max(memoryBandwidth); fprintf('Peak read/write speed on the GPU is %g GB/s\n',maxBWGPU)
Peak read/write speed on the GPU is 110.993 GB/s
To know whether this is fast or not, I compare it with the same code running on the CPU. Note, however, that the CPU has several levels of caching and some oddities like "read before write" that can make the results look a little odd. For my PC the theoretical bandwidth of main memory is 32GB/s, so anything above this is likely to be due to efficient caching.
memoryTimesHost = inf(size(sizes)); for ii=1:numel(sizes) numElements = sizes(ii)/sizeOfDouble; for rr=1:repeats hostData = zeros(numElements,1); timer = tic(); for jj=1:100 hostData = hostData + 1; end memoryTimesHost(ii) = min(memoryTimesHost(ii), toc(timer)/100); end end memoryBandwidthHost = 2*(sizes./memoryTimesHost)/1e9; [maxBWHost, maxBWHostIdx] = max(memoryBandwidthHost); fprintf('Peak write speed on the host is %g GB/s\n',maxBWHost) % Plot CPU and GPU results. hold off semilogx(sizes, memoryBandwidth, 'b.-', ... sizes, memoryBandwidthHost, 'k.-') hold on semilogx(sizes(maxBWIdxGPU), maxBWGPU, 'bo-', 'MarkerSize', 10); semilogx(sizes(maxBWHostIdx), maxBWHost, 'ko-', 'MarkerSize', 10); grid on title('Read/Write Bandwidth') xlabel('Array size (bytes)') ylabel('Speed (GB/s)') legend('Read+Write (GPU)','Read+Write (host)','Location','NorthWest')
Peak write speed on the host is 44.6868 GB/s

It is clear that GPUs can read and write their memory much faster than they can get data from the host. Therefore, when writing code you must minimize the number of host-GPU or GPU-host transfers. You must transfer the data to the GPU, then do as much with it as possible whilst on the GPU, and only bring it back to the host when you absolutely need to. Even better, create the data on the GPU to start with if you can.
Test Computation-Intensive Calculations
For operations where computation dominates, the memory speed is much less important. In this case you are probably more interested in how fast the computations are performed. A good test of computational performance is a matrix-matrix multiply. For multiplying two NxN matrices, the total number of floating-point calculations is
$FLOPS(N) = 2N^3 - N^2$
As above, I time this operation on both the host PC and the GPU to see their relative processing power:
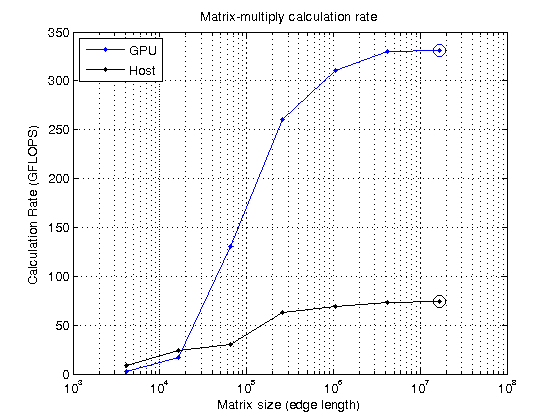
sizes = power(2, 12:2:24); N = sqrt(sizes); mmTimesHost = inf(size(sizes)); mmTimesGPU = inf(size(sizes)); for ii=1:numel(sizes) A = rand( N(ii), N(ii) ); B = rand( N(ii), N(ii) ); % First do it on the host for rr=1:repeats timer = tic(); C = A*B; %#ok<NASGU> mmTimesHost(ii) = min( mmTimesHost(ii), toc(timer)); end % Now on the GPU A = gpuArray(A); B = gpuArray(B); for rr=1:repeats timer = tic(); C = A*B; %#ok<NASGU> wait(gpu); mmTimesGPU(ii) = min( mmTimesGPU(ii), toc(timer)); end end mmGFlopsHost = (2*N.^3 - N.^2)./mmTimesHost/1e9; [maxGFlopsHost,maxGFlopsHostIdx] = max(mmGFlopsHost); mmGFlopsGPU = (2*N.^3 - N.^2)./mmTimesGPU/1e9; [maxGFlopsGPU,maxGFlopsGPUIdx] = max(mmGFlopsGPU); fprintf('Peak calculation rate: %1.1f GFLOPS (host), %1.1f GFLOPS (GPU)\n', ... maxGFlopsHost, maxGFlopsGPU)
Peak calculation rate: 73.7 GFLOPS (host), 330.9 GFLOPS (GPU)
Now plot it to see where the peak was achieved.
hold off semilogx(sizes, mmGFlopsGPU, 'b.-', sizes, mmGFlopsHost, 'k.-') hold on semilogx(sizes(maxGFlopsGPUIdx), maxGFlopsGPU, 'bo-', 'MarkerSize', 10); semilogx(sizes(maxGFlopsHostIdx), maxGFlopsHost, 'ko-', 'MarkerSize', 10); grid on title('Matrix-multiply calculation rate') xlabel('Matrix size (edge length)') ylabel('Calculation Rate (GFLOPS)') legend('GPU','Host','Location','NorthWest')
Comparing GPUs
After measuring both the memory bandwidth and calculation performance, I can now compare my GPU to others. Previously I ran these tests on a couple of different GPUs and stored the results in a data-file.
offline = load('gpuBenchmarkResults.mat'); names = ['This GPU' 'This host' offline.names]; ioData = [maxBWGPU maxBWHost offline.memoryBandwidth]; calcData = [maxGFlopsGPU maxGFlopsHost offline.mmGFlops]; subplot(1,2,1) bar( [ioData(:),nan(numel(ioData),1)]', 'grouped' ); set( gca, 'Xlim', [0.6 1.4], 'XTick', [] ); legend(names{:}) title('Memory Bandwidth'), ylabel('GB/sec') subplot(1,2,2) bar( [calcData(:),nan(numel(calcData),1)]', 'grouped' ); set( gca, 'Xlim', [0.6 1.4], 'XTick', [] ); title('Calculation Speed'), ylabel('GFLOPS') set(gcf, 'Position', get(gcf,'Position')+[0 0 300 0]);

Conclusions
These tests reveal a few things about how GPUs behave:
- Transfers from host memory to GPU memory and back are relatively slow, <6GB/s in my case.
- A good GPU can read/write its memory much faster than the host PC can read/write its memory.
- Given large enough data, GPUs can perform calculations much faster than the host PC, more than four times faster in my case.
Noticable in each test is that you need quite large arrays to fully saturate your GPU, whether limited by memory or by computation. You get the most from your GPU when working with millions of elements at once.
If you are interested in a more detailed benchmark of your GPU's performance, have a look at GPUBench on the MATLAB Central File Exchange.
If you have questions about these measurements or spot something I've done wrong or that could be improved, leave me a comment here.
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.