Uniqueness and Membership
We have had many requests over the years for some of our functions to include tolerances, e.g., find. I don't know if you noticed, but some of the relevant functions (not find) now allow this.
Contents
uniquetol and ismembertol
Recently (R2015a), we added ismembertol and uniquetol to MATLAB. This is to reflect the notion that, especially with floating point arithmetic, we should not generally expect quantities that we compare to be exact matches, but close, to within an tolerance. You can argue that |find|ing something might sound a bit more specific, hence no tolerance there. Not sure if that holds up. And, of course, there's always eps. So now there are some more good tools for you to use!
Specify Data Scaling by Column
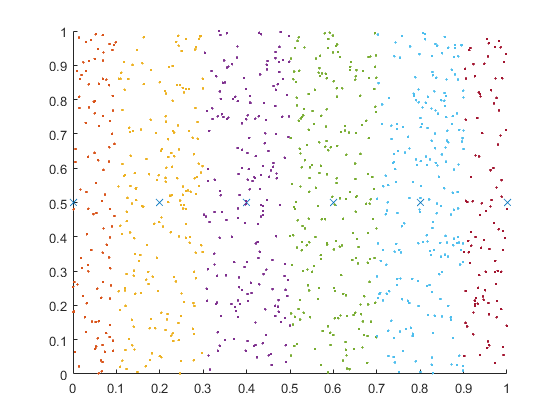
Let's suppose we have some data that we want to group into different vertical bands. The rows of A and B contain the x and y values of the points. Because of this, we set 'ByRows' to be true. And we want all points included; hence 'OutputAllIndices' is also true. Finally we use the 'DataScale' to be unbounded at the high end for y so we can ignore those values, but 1 for an absolute tolerance for x.
A = rand(1000,2); B = [(0:.2:1)',0.5*ones(6,1)]; [LIA,LocAllB] = ismembertol(B, A, 0.1, 'ByRows', true, ... 'OutputAllIndices', true, 'DataScale', [1,Inf])
LIA =
1
1
1
1
1
1
LocAllB =
[103x1 double]
[185x1 double]
[188x1 double]
[213x1 double]
[212x1 double]
[ 99x1 double]
You can see we get several bands of data, with different amounts in each bin of LocallB.
Plot the Results
Now we want to plot the points in A that are within the distance of the stated tolerance for each point in B.
hold on plot(B(:,1),B(:,2),'x') for k = 1:length(LocAllB) plot(A(LocAllB{k},1), A(LocAllB{k},2),'.') end hold off
Your Turn
Have you found good uses for these new functions that let you look for relevant candidates within some tolerance? Let me know here.
- Category:
- New Feature
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.