Today I introduce guest blogger Arkadiy Turevskiy to share some new features in R2009b: the PID Controller Blocks in Simulink and a new PID tuning method in Simulink Control Design.

PID (Proportional-Integral-Derivative) control seems easy: you just need to find three numbers: proportional, integral, and derivative gains. Many PID tuning rules exist out there and all you need to do is pick up one and press a button on a calculator. Easy enough, right? Unfortunately, the story is more complicated than that. Popular PID tuning methods are restrictive. For example, to use one of the most popular methods - Ziegler-Nichols - you need a stable, first order plus dead-time linear time-invariant (LTI) plant model. Even if your model is of that type, the method does not support tuning of integral or proportional-derivative controllers, and for the types of PID controllers it supports, it only provides one answer with no easy way to fine-tune the design. Moreover, tuning is not the only challenge. Real-life PID implementation also needs to consider such issues as output saturation, integrator wind-up, and discrete-time implementation.

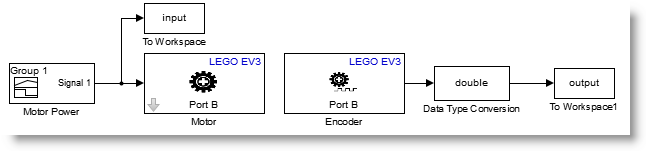
In R2009b we released new blocks in Simulink and a new PID tuning method in Simulink Control Design that together address these challenges. To see how this works, let’s consider an example of designing a PID controller for a dc motor. The model of a closed loop system uses the new PID Controller block. This block generates a voltage signal driving the dc motor to track desired shaft rotation speed. In addition to voltage, the dc motor subsystem takes torque disturbance as an input, allowing us to simulate how well the controller rejects disturbances. We also modeled analog sensor noise in the speed measurement.

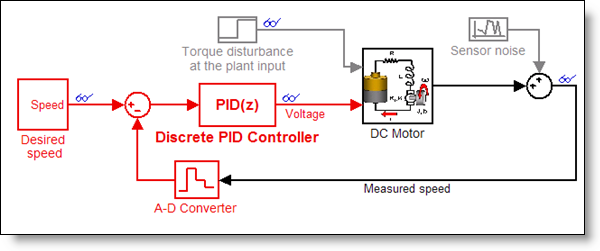
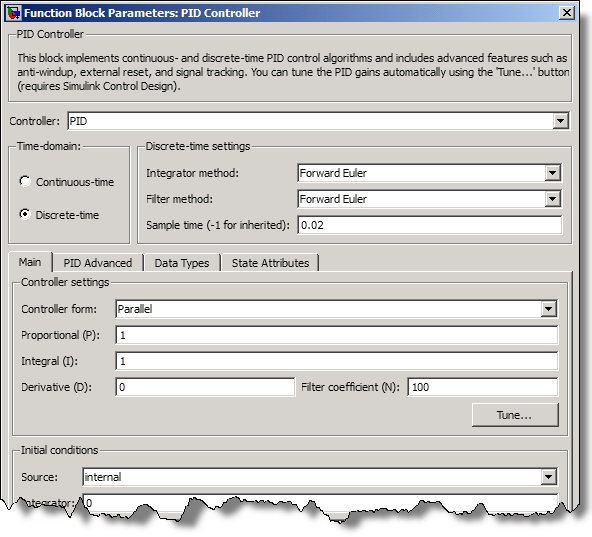
The PID controller is a discrete-time controller running at 0.02 seconds (the red color shows the sampling time in the model). Let’s now look at the dialog of the PID Controller block. In the upper half of the dialog we specified basic configuration of the PID controller: type (PID, PI, PD, P, or I), time-domain, integration methods, and sample time. In the lower part, we specified PID controller form and gains (shown at default values).  Block documentation provides detailed information about the block and all its parameters.

PID Tuning

Our first task is to tune the PID controller. Pressing the “Tune…” button in the PID Controller block dialog, we launch PID Tuner, which linearizes the model at the default operating point and automatically determines PID controller gains to achieve reasonable performance and robustness based on linearized plant model.

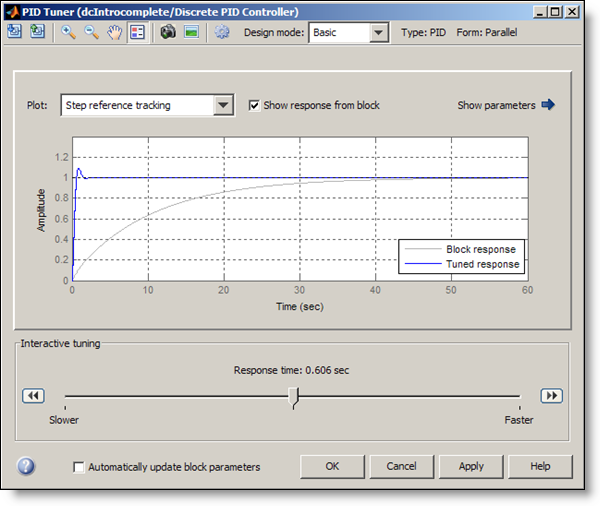
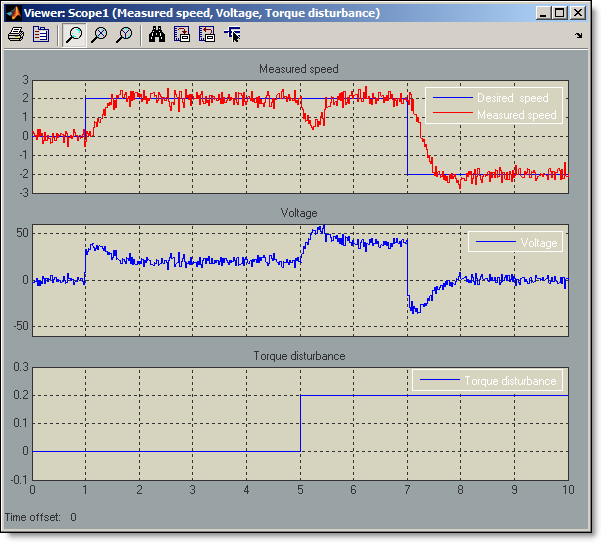
The grey line shows the system step response for the gain values currently defined in the block dialog, and the blue line shows the system response for the gain values that PID Tuner proposes. We can simply accept the proposed design and then run our closed-loop Simulink model to check the results. In the simulation, we command a step change from 0 to 2 rpm at 1 second and a step down to -2 rpm at 7 seconds. Results demonstrate good tracking with zero steady-state error, fast rise time, low overshoot, and good torque disturbance rejection (torque disturbance is modeled as a step change from 0 to 0.2 Newton-meters at 5 seconds). The tuning algorithm we just used works on any type of plant model, tunes all forms of PID controllers that can be specified in the PID Controller block, and takes sampling effects into account during the tuning process.

If system response does not meet our requirements, we could further fine-tune the design by interactively making the controller faster or slower, using the slider on the bottom of the PID Tuner GUI.

Integrator Anti-Windup Protection

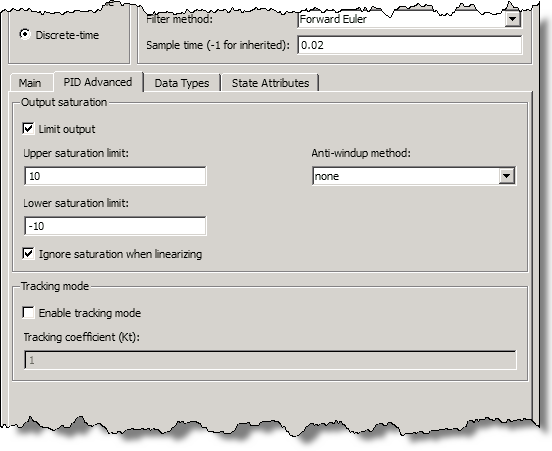
We now run a different scenario, assuming no torque disturbance and assuming that the amplitude of voltage fed to the dc motor cannot exceed 10 Volts – to protect the motor from overheating. We use the “PID Advanced” tab of the PID Controller block dialog to specify these saturation limits.

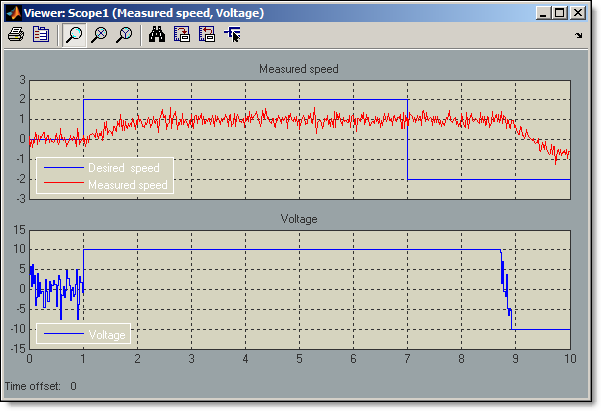
We see that at the time of the first step change at 1 second, voltage signal from the controller saturates at 10 Volts.  When desired speed drops at 7 seconds, the voltage does not decrease immediately and stays at 10 Volts for almost 2 more seconds.  This is the result of integrator wind-up in PID controller, which leads to undesired delay in tracking the speed command.  It can be fixed by enabling integrator anti-windup in the PID Controller block dialog. Rerunning the simulation with integrator anti-windup enabled, we see that the controller still cannot achive commanded speed value of 2 rpms –it simply does not have enough authority, but when the speed is commanded to -2 rpms, controller quickly responds to change in the requested speed.

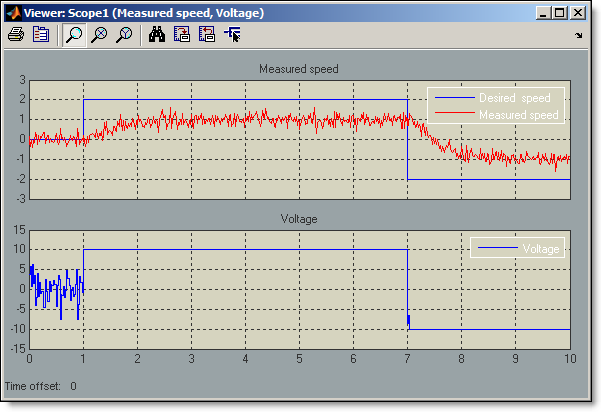
As we saw, the new PID tuning method and the new PID Controller block helped us quickly tune our PID Controller, and create a discrete-time design that addresses output saturation and integrator wind-up issues.

Now it is your turn

Do you use PID control? How do you address integrator wind-up?  Leave a comment here and tell us how you tune your controller gains.