The QR algorithm is one of the world's most successful algorithms. We can use animated gifs to illustrate three variants of the algorithm, one for computing the eigenvalues of a nonsymmetric... read more >>

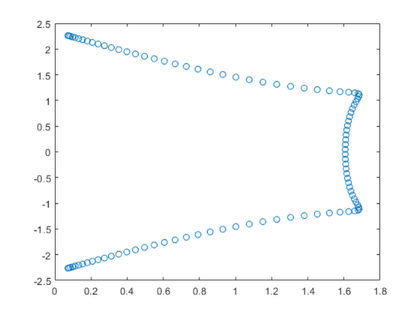
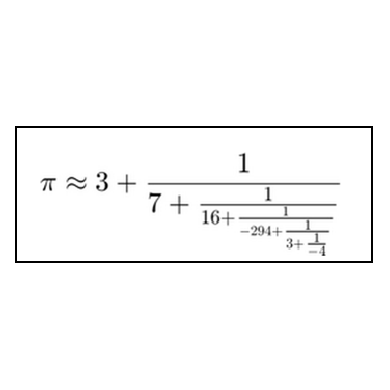
I have just returned from the ICIAM2019 conference in Valencia, Spain. It was a huge conference -- 4,000+ attendees, dozens of prize and invited talks, hundreds of parallel minisympsia. I gave a talk in a two-part minisymposium organized by Nick Higham and Rob Corless. I outlined the first part of the talk in this blog a month ago. This post outlines the second part, which was about Hadamard matrices. Some of it is taken from a post in this blog five years ago.... read more >>

(This is a reprint of the second ever Cleve's Corner from the Winter 1990 MathWorks Newsletter).The other day at lunch with a couple of other MathWorks people, I posed the following... read more >>

We will have a two-part minisymposium on "Bohemian Matrices" at ICIAM2019, the International Congress on Industrial and Applied Mathematics in Valencia, Spain, July 15-19. This is an outline of my talk.... read more >>

This is a summary of my talk at the conference Celebrating the Centenary of James H. Wilkinson's Birth at the University of Manchester, May 29.... read more >>

On May 29-30, I plan to attend a conference, organized by Nick Higham, at the University of Manchester. The title of the conference is... read more >>

Let me tell you about MATLAB's controversial function rat.... read more >>

This post is by my colleague Cosmin Ionita.... read more >>

Why are manhole covers round? It is so they won't fall through the hole they are intended to cover. They have the same diameter regardless of where it is measured. If the hole has a slightly smaller diameter, it is not possible to orient the cover so that it will fall through. A square or rectangular cover can be turned slightly and it will easily fit through the hole.... read more >>

Sedona Arizona is a perfect site for the first MathWorks excursion into lifestyle products.... read more >>