Text Mining Machine Learning Research Papers with MATLAB
Publish or perish, they say in academia, and you can learn trends in academic research through analysis of published papers. Today's guest blogger, Toshi, came across a dataset of machine learning papers presented in a conference. Let's see what he found!

Contents
NIPS 2015 Papers
NIPS (which stands for "Neural Information Processing Systems") is an annual conference on machine learning and computational neuroscience, and papers presented there reveal what experts in the field are working on. Conveniently, you can find the data from the 2015 conference from Kaggle's NIPS 2015 Papers page.
Let's load the data downloaded from Kaggle to the current folder. Kaggle provides an SQLite database file in addition to usual CSV files and the SQLite file contains all the data in CSV files. Since we now have configuration-free SQLite support in Database Toolbox in R2016a, let's give that a try. Once you establish a connection to the databasefile with sqlite, you can use SQL commands like '|SELECT * FROM Authors|'. For more details about SQLite support, read Working with the MATLAB Interface to SQLite. If you don't have Database Toolbox, you can try readtable to read CSV files.
I also wrote a script nips2015_parse_html in order to parse the HTML file "accepted_papers.html" that contains the affiliation of the authors. Check it out if you are interested in data wrangling with MATLAB.
db = 'output/database.sqlite'; % database file conn = sqlite(db,'readonly'); % create connection Authors = fetch(conn,'SELECT * FROM Authors'); % get data with SQL command Papers = fetch(conn,'SELECT * FROM Papers'); % get data with SQL command PaperAuthors = fetch(conn,'SELECT * FROM PaperAuthors'); % get data with SQL command close(conn) % close connection Authors = cell2table(Authors,'VariableNames',{'ID','Name'});% convert to table Papers = cell2table(Papers,'VariableNames', ... % convert to table {'ID','Title','EventType','PdfName','Abstract','PaperText'}); PaperAuthors = cell2table(PaperAuthors,'VariableNames', ... % convert to table {'ID','PaperID','AuthorID'}); html = fileread('output/accepted_papers.html'); % load text from html nips2015_parse_html % parse html text
Paper Author Affiliation
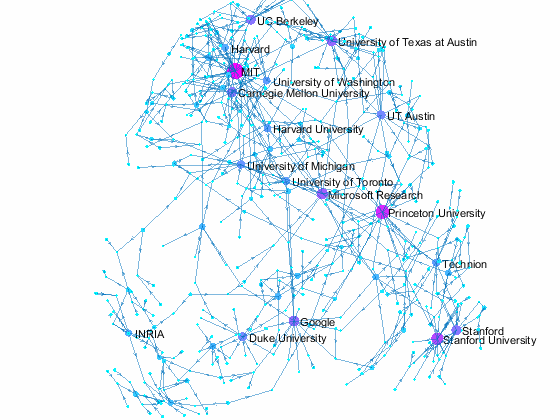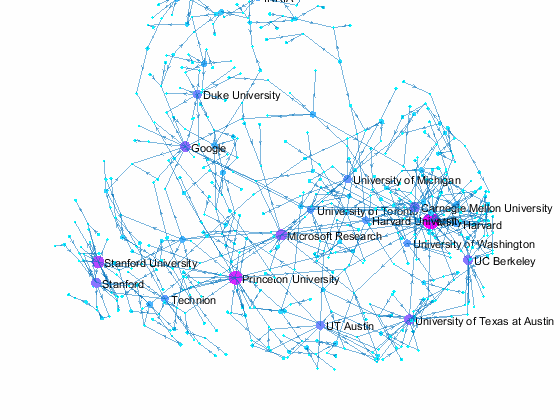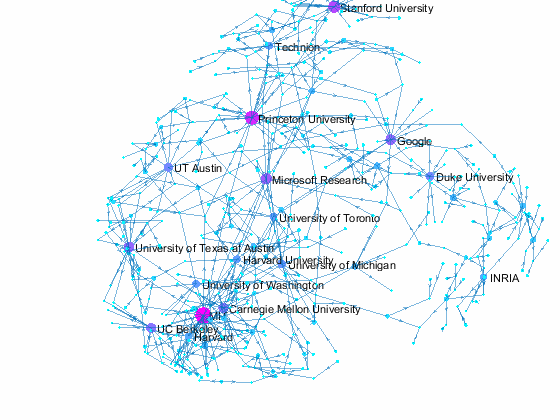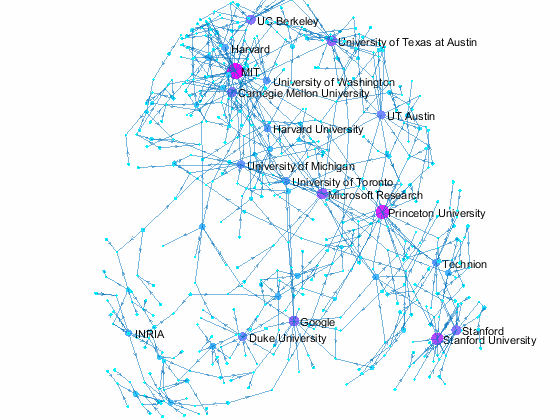
We can visualize which organization the authors of accepted papers belong to using graphs. Let's create a directed graph with authors and their affiliation as nodes. We limit the plot to organizations with 10 or more authors, but some smaller organizatoins are also included if authors have multiple affiliations that include smaller organizations. The top 20 organizations, in terms of number of affiliated authors, are colored in bright orange while others are colored in a yellowish orange. Small blue dots are individual authors. This is just based on papers from one conference in 2015, so the top ranking organizations may be different from year to year.
T = AcceptedPapers(:,{'Name','Org'}); % subset table
[T, ~, idx] = unique(T,'rows'); % remove duplicates
auth = T.(1); % authors
org = cellstr(T.(2)); % organizations
w = accumarray(idx, 1); % count of papers
G = digraph(auth,org,w); % create directed graph
G.Nodes.Degree = indegree(G); % add indegree
bins = conncomp(G,'OutputForm','cell','Type','weak'); % get connected components
binsizes = cellfun(@length,bins); % get bin sizes
small = bins(binsizes < 10); % if bin has less than 10
small = unique([small{:}]); % it is small
G = rmnode(G, small); % remove nodes in the bin
org = G.Nodes.Name(ismember(G.Nodes.Name,org)); % get org nodes
deg = G.Nodes.Degree(ismember(G.Nodes.Name,org)); % get org node indegrees
[~, ranking] = sort(deg,'descend'); % rank by indegrees
topN = org(ranking(1:20)); % select top 20
others = org(~ismember(org,topN)); % select others
markersize = log(G.Nodes.Degree + 2)*3; % indeg for marker size
linewidth = 5*G.Edges.Weight/max(G.Edges.Weight); % weight for line width
figure % create new figure
h = plot(G,'MarkerSize',markersize,'LineWidth',linewidth,'EdgeAlpha',0.3); % plot graph
highlight(h, topN,'NodeColor',[.85 .33 .1]) % highlight top 20 nodes
highlight(h, others,'NodeColor',[.93 .69 .13]) % highlight others
labelnode(h,org,org) % label nodes
title({'NIPS 2015 Paper Author Affiliation';'with 10 or more authors'}) % add title

Paper Coauthorship
Coauthors of a paper may come from different organizations, and this gives us an opportunity to see the relationship among those organizations. Let's create a directed graph with authors and their papers as nodes. We limit the plot to a cluster of organizations with 5 or more nodes by separating the graph into connnected components with conncomp. The same top 20 organizations in terms of number of affiliated authors are again colored in bright orange while others are colored in a yellowish orange. Interestingly, the plot shows that all orange dots are located in the same cluster - so all top 20 organizations belong to a network of coauthors. Again, this is based on papers from a single conference, so the results may be very different for other years. If we track paper coauthorship over multiple years, we may find some hidden connections that we don't see here.
T = AcceptedPapers(:,{'Org','Title'}); % subset table
[T, ~, idx] = unique(T,'rows'); % remove duplicates
org = cellstr(T.(1)); % organizations
paper = T.(2); % papers
w = accumarray(idx, 1); % count of papers
G = digraph(paper,org,w); % create directed graph
G.Nodes.Degree = indegree(G); % add indegree
bins = conncomp(G,'OutputForm','cell','Type','weak'); % get connected components
binsizes = cellfun(@length,bins); % get bin sizes
small = bins(binsizes < 5); % if bin has less than 5
small = unique([small{:}]); % it is small
G = rmnode(G, small); % remove nodes in the bin
org = G.Nodes.Name(ismember(G.Nodes.Name,org)); % get org nodes
[~,maxBinIdx] = max(binsizes); % index of largest component
topDocs = setdiff(bins{maxBinIdx},org); % get docs in largest component
isTopDoc = ismember(AcceptedPapers.Title,topDocs); % get indices of those docs
topDocIds = unique(AcceptedPapers.PaperID(isTopDoc)); % get the paper ids of those docs
isTopDoc = ismember(Papers.ID,topDocIds); % get indices of those docs
markersize = log(G.Nodes.Degree + 2)*3; % get org nodes
linewidth = 10*G.Edges.Weight/max(G.Edges.Weight); % indeg for marker size
figure % create new figure
h = plot(G,'MarkerSize',markersize,'LineWidth',linewidth,'EdgeAlpha',0.3); % plot graph
highlight(h, topN,'NodeColor',[.85 .33 .1]) % highlight top 20 nodes
others = org(~ismember(org,topN)); % select others
highlight(h, others,'NodeColor',[.93 .69 .13]) % highlight others
labelnode(h,topN(1),'Top 20') % label nodes
labelnode(h,others([1,4,18,29,72,92,96,99]),'Others') % label nodes
title({'NIPS 2015 Paper Coauthorship By Affiliation';'with 5 or more nodes'}) % add title

Paper Topics
To find the topics of the papers, I quickly went through the titles of the accepted papers and chose 35 words that jumped out at me - see nips2015_topics.xlsx. If you check the word cloud at the top, you see some of those words. Obviously, this is a quick-and-dirty approach but I just wanted to get a quick sense of the popular topics for now. If you are interested in a more proper way to do it, please check out my earlier post Can You Find Love through Text Analytics?
The paper table contains Title, Abstract and PaperText columns. Which should we use to analyze the paper topics? Titles tend to be short. Abstracts are longer, and are more likely to contain key phrases that represent the paper topic because abstracts are, by definition, a high level overview of the content of the paper. Actual content of the paper naturally covers more details and that may obscure the main topics of the paper. Let's use Abstract to generate our word count.
Then let's compare the relative frequency of those terms between the docs in the largest connected component we saw earlier and other docs. You can see some differences between those two groups. For example, a lot of pagers discuss 'image', but papers from the top 20 organizations talk about it less frequently, and they talk more about 'graph'.
Topics = readtable('nips2015_topics.xlsx'); % load preselected topics DTM = zeros(height(Papers),height(Topics)); % document term matrix for i = 1:height(Topics) % loop over topics DTM(:,i) = cellfun(@length, ... % get number of matches regexpi(Papers.Abstract,Topics.Regex{i})); % find the word in abstract end topDocTopics = sum(DTM(isTopDoc,:)); % word count in largest component topDocTopics = topDocTopics ./ sum(topDocTopics) *100; % convert it into relative percentage otherDocTopics = sum(DTM(~isTopDoc,:)); % word count in others otherDocTopics = otherDocTopics ./ sum(otherDocTopics) *100;% convert it into relative percentage figure % create new figure bar([topDocTopics; otherDocTopics]') % bar chart ax = gca; % get current axes handle ax.XTick = 1:height(Topics); % set X-axis tick ax.XTickLabel = Topics.Keyword; % set X-axis tick label ax.XTickLabelRotation = 90; % rotate X-axis tick label title('Relative Term Frequency by Document Groups') % add title legend('Docs in the Largest Cluster','Other Docs') % add legend xlim([0 height(Topics) + 1]) % set x-axis limits ylabel('Percentage') % add y-axis label

Topic Grouping by Principal Componet Analysis
Let's visualize the relationship between topics using Principal Component Analysis. The resulting biplot of the first and second components shows roughly three clusters of related topics. Topics popular in the largest connected component are highlighted in orange and they seem to span across all three clusters.
The purple cluster is dominated by topics favored by the largest connected component and focuses on topics likes Markov Chain Monte Carlo (MCMC), Bayesian Statistics and Stochastic Gradient MCMC.
The blue cluster seems to focus on the multi-armed bandits problem which is related to a field of machine learning called Reinforcement Learning. Topics like 'market' and 'risk' are highlighted in orange, indicating that papers on these topics from the top 20 organizations probably focused on financial applications.
w = 1 ./ var(DTM); % inverse variable variances [wcoeff, score, latent, tsquared, explained] = ... % weighted PCA with w pca(DTM, 'VariableWeights', w); coefforth = diag(sqrt(w)) * wcoeff; % turn wcoeff to orthonormal labels = Topics.Keyword; % Topics as labels topT = Topics.Keyword((topDocTopics - otherDocTopics) > 1); % topics popular in top cluster figure % new figure biplot(coefforth(:,1:2), 'Scores', score(:,1:2), ... % 2D biplot with the first two comps 'VarLabels', labels) title('Principal Components Analysis of Paper Topics') % add title for i = 1:length(topT) % loop over popular topics htext = findobj(gca,'String',topT{i}); % find text object htext.Color = [.85 .33 .1]; % highlight by color end rectangle('Position',[.05 -.1 .5 .3],'Curvature',1, ... % add rectagle 'EdgeColor',[0 .5 0]) rectangle('Position',[-.23 .05 .25 .55],'Curvature',1, ... % add rectangle 'EdgeColor',[.6 .1 .5]) rectangle('Position',[-.35 -.4 .34 .42],'Curvature',1, ... % add rectangle 'EdgeColor',[.1 .2 .6])

Deep Learning
The green cluster is very busy and hard to see. Let's zoom into the green cluster to see more details using axis. Deep learning seems to be the main topic of this cluster. CNN (Convolutional Neural Networks) is a deep learning algorithm often used for image classification. It makes sense that it is close to the 'image' topic in the biplot. RNN (Recurrent Neural Networks) tends to be used in Natural Language Processing and it appears close to 'text'. Autoencoders and LSTM (Long Short-Term Memory) are also deep learning algorithms. MAP (Maximum A Posteriori) and 'deep neural networks' are the only topics popular in the top 20 organizations that are found in this cluster. Because we are just comparing the relative frequency of word occurrence, if a lot of papers talk about deep learning related topics, then there are barely any significant frequency differences between the top 20 and others, and those words won't be highlighted.
axis([-0.1 0.5 -0.1 0.2]); % define axis limits

Core Algorithms
The topics found at the center of the biplot are related to more established core machine learning techniques such as Support Vector Machines (SVM), Principal Component Analysis (PCA), Hidden Markov Models (HMM) or Least Absolute Shrinkage And Selection Operator (LASSO). Papers from the top 20 organizations seem be interested in tensors and multi-class classification problems, along with graphs and Gaussian Process.
axis([-0.06 0.06 -0.06 0.06]); % define axis limits

Commercial Research
The top 20 organizations include some commercial entities such as Google, IBM and Microsoft. The topics of their research papers probably reflects commercial interests in the field of machine learning. We can use the same biplot and highlight the topics that frequently appear in the papers affiliated with them. The plot shows that the three companies tend to cover different topics while they all engage in some deep learning related research. You can also see that Google tends to cover multiple fields while IBM and Microsft seem to have a narrower focus.
isGoogler = AcceptedPapers.Org == 'Google'; % find indices of Google authors GooglePaperIds = unique(AcceptedPapers.PaperID(isGoogler)); % find their paper ids isGooglePaper = ismember(Papers.ID,GooglePaperIds); % get the paper indices GoogleTopics = sum(DTM(isGooglePaper,:)); % sum Google rows GoogleTopics = GoogleTopics ./ sum(GoogleTopics) *100; % convert it into relative percentage isIBMer = AcceptedPapers.Org == 'IBM'; % find indices of IBM authors IBMPaperIds = unique(AcceptedPapers.PaperID(isIBMer)); % find their paper ids isIBMPaper = ismember(Papers.ID,IBMPaperIds); % get the paper indices IBMTopics = sum(DTM(isIBMPaper,:)); % sum IBM rows IBMTopics = IBMTopics ./ sum(IBMTopics) *100; % convert it into relative percentage isMSofter = AcceptedPapers.Org == 'Microsoft'; % find indices of Mirosoft authors MSPaperIds = unique(AcceptedPapers.PaperID(isMSofter)); % find their paper ids isMSPaper = ismember(Papers.ID,MSPaperIds); % get the paper indices MSTopics = sum(DTM(isMSPaper,:)); % sum Microsoft rows MSTopics = MSTopics ./ sum(MSTopics) *100; % convert it into relative percentage commercialTopics = [GoogleTopics; IBMTopics; MSTopics]; % combine all figure % new figure biplot(coefforth(:,1:2), 'Scores', score(:,1:2), ... % 2D biplot with the first two comps 'VarLabels', labels) hline = findobj(gca,'LineStyle','none'); % get line handles of observations for i = 1:length(hline) % loop over observatoins hline(i).Visible = 'off'; % make it invisible end htext = findobj(gca,'Type','text'); % get text handles tcolor = [0 .5 0;.85 .33 .1; .1 .2 .6]; % define text color for i = 1:length(htext) % loop over text r = commercialTopics(:,strcmp(labels,htext(i).String)); % get ratios if sum(r) == 0 % if all rows are zero htext(i).Visible = 'off'; % make it invisible else % otherwise [~,idx] = max(r); % get max row htext(i).Color = tcolor(idx,:); % use matching color end end text(-.4,.3,'Google','Color',tcolor(1,:),'FontSize',14) % annotate text(.3,-.1,'IBM','Color',tcolor(2,:),'FontSize',14) % annotate text(-.4,-.2,'Microsoft','Color',tcolor(3,:),'FontSize',14) % annotate title({'Principal Components Analysis of Paper Topics'; % add title 'highlighting Google, IBM and Microsoft topics'})

Top 10 Authors in NIPS 2015
Some authors got multiple papers accepted by NIPS. Are there any specific topics that gives them an edge? Let's take a look at the top 10 authors in terms of number of accepted papers and see what topics come up in those papers. It turns out the topics of the op 10 authors don't belong to specifc clusters, and the vectors of those topics are shorter - meaning they are not so uncommon but not as frequently discussed as other topics, such as 'bandits', 'CNN' or 'MCMC', either.
[auth_ids,~,idx] = unique(AcceptedPapers.ID); % get author ids count = accumarray(idx,1); % get count [~,ranking] = sort(count,'descend'); % get ranking top10_ids = auth_ids(ranking(1:10)); % get top 10 ids isTop10 = ismember(AcceptedPapers.ID,top10_ids); % get row indices top10_paper_ids = unique(AcceptedPapers.PaperID(isTop10)); % get top 10 papaer ids isTop10paper = ismember(Papers.ID,top10_paper_ids); % get row indices top10Topics = sum(DTM(isTop10paper ,:)); % sum top 10 rows top10Topics = top10Topics ./ sum(top10Topics) *100; % convert it into relative percentage notTop10Topics = sum(DTM(~top10Topics,:)); % word count in others notTop10Topics = notTop10Topics ./ sum(notTop10Topics) *100;% convert it into relative percentage combined = [top10Topics;notTop10Topics]; % combine all [isTop10Author,order] = ismember(Authors.ID,top10_ids); % get indices of top 10 authors [~,order] = sort(order(isTop10Author)); % get ranking names = Authors.Name(isTop10Author); % get names figure % create new figure biplot(coefforth(:,1:2), 'Scores', score(:,1:2), ... % 2D biplot with the first two comps 'VarLabels', labels) hline = findobj(gca,'LineStyle','none'); % get line handles of observations for i = 1:length(hline) % loop over observatoins hline(i).Visible = 'off'; % make it invisible end htext = findobj(gca,'Type','text'); % get text handles tcolor = [.85 .33 .1; .1 .2 .6]; % define text color for i = 1:length(htext) % loop over text r = combined(:,strcmp(labels,htext(i).String)); % get ratios [~,idx] = max(r); % get max row if idx == 1 && r(1) > 3 % if row 1 & r > 3 htext(i).Color = [.85 .33 .1]; % highlight text else htext(i).Color = [.6 .6 .6]; % ghost text end end title({'Principal Components Analysis of Paper Topics'; % add title 'highlighting topics by top 10 authors'}) text(-.5,.3,'Top 10 ','FontWeight','bold') % annotate text(-.5,0,names(order)) % annotate

Summary
This is a fairly simple, quick exploration of the dataset, but we got some interesting insights about the current state of machine learning research presented at NIPS 2015. Maybe you can find even more if you dig deeper. Perhaps you can use the technique in the post Can You Find Love through Text Analytics? to cluster similar papers. You can use word-based tokens, but you may want to use an n-gram approach described in another post, Text Mining Shakespeare with MATLAB. Give it a try and share your findings here!
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.