Today I'd like to welcome a guest blogger, Mike Croucher, who recently joined MathWorks as a Customer Success Engineer after a long career spent supporting academic computational research. Introduction
Most of my career has been dedicated to collaborating with scientists and engineers to improve their computational workflows. There are many things that could be done including encouraging the use of version control or unit testing but, by far, the most frequent request has been 'Can you make this thing I made go any faster?' At its core, the art of making a program faster comes down to iterating over two simple steps.
- Find out exactly what is slow.
- Try something different to see if it's any faster while still giving the right answer
As you might imagine, there's a world of complexity hidden in the above. 'Trying something different' could mean using language features to optimise the algorithm I've written, trying out parallelisation or even switching to a completely different algorithm althogether. I usually add an additional constraint to point 2 which is 'expend as little effort as possible' because I am fundamentally lazy.
Of course there are always times when we need to optimise our code for speed and I wanted to share an example that was recently discussed internally.
Don't Fear the Looper
type myCountPrimes.m
% Count how many primes there are up to and including max_n
function res = myCountPrimes(max_n)
res = 0;
for i = 2:max_n
if MyIsPrime(i)
res = res+1;
end
end
end
% Function to check if n is prime
function result = MyIsPrime(n)
if n <= 1
result = false;
return
end
q = floor(sqrt(n));
for i = 2:q
if mod(n,i) == 0
result = false;
return
end
end
result = true;
end
numPrimes = myCountPrimes(1000000)
f = @() myCountPrimes(1000000);
originalSpeed = timeit(f)
Even so, there are many things we could try to speed up this particular piece of code. We could take advantage of the fact that every iteration of the loop in myCountPrimes is independent and use a parallel parfor loop. This is easy to do but might be heavy on computational resources. Once you realise you can leverage parfor, it becomes tempting to try to make your problem go away by throwing as many CPU cores as you possible at it. My favourite way to do this these days is to fire up a Cloud Center cluster and ramp up the core count as high as makes sense. Changing mod to floor
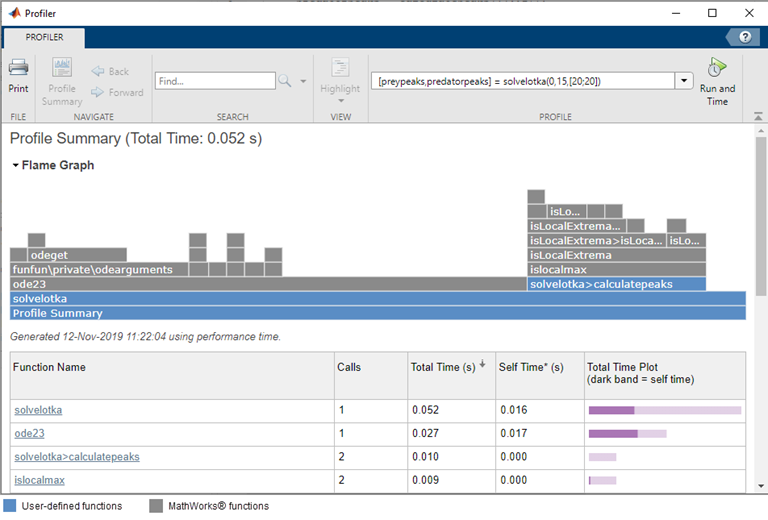
The profiler showed me that a lot of time was spent in the line
if mod(n,i) == 0
so one approach is to ask 'Can we rewrite that line to be any faster?'. It's not always obvious which alternatives might work so I often simply figure out a different way to do something and give it a try. An alternative way to write the expression mod(n,i)==0 is floor(n/i) == n/i and it turns out to be much faster! I did this in the floorMyCountPrimes function, checked that it gives the right result, and demonstrated that it is indeed much faster.
numPrimes = floorMyCountPrimes(1000000)
f = @() floorMyCountPrimes(1000000);
Trying Integer Types for an Integer Algorithm
By default, all numbers in MATLAB are floating point of type double which is great for a lot of numerical computing but here we are dealing with a purely integer algorithm. It can sometimes pay dividends to make this explicit in the code and this is one of those times! It turns out that the mod function has to do a lot more work when dealing with floating point numbers than is strictly necessary for this particular example. As the programmer, I know that my algorithm is completely integer based so I can switch to using uint32 for some variables. That is, I change the main loop of MyIsPrime to
This allows MATLAB to use a specialised and faster version of the mod function since it now knows that we are dealing with integers instead of doubles.
I did this in the uint32MyIsPrime function defined at the end of this post and called it via uint32MyCountPrimes. First let's check that the result agrees with the original function and then time it
numPrimes = uint32MyCountPrimes(1000000)
f = @() uint32MyCountPrimes(1000000);
Using either this approach or the floor-based approach, we achieved a significant performance boost for relatively little work and techniques such as parfor parallelisation are still on the table if we need even more speed.
MATLAB as a Repository of Algorithms
Finally, we could recognise that the fundamental algorithm we are using to count primes is not optimal and use a different one instead. Taking this to the extreme, we could remember that MATLAB is a repository of numerical algorithms as well as a programming language and so find the one that directly solves the problem we want to solve rather than rolling our own. A quick search of the documentation reveals the primes function that returns an array of primes. We produce this array and count the elements as follows. numPrimes = numel(primes(1000000))
f = @() numel(primes(1000000));
More than fast enough for my purposes!
System Information
If you run this script on your own machine, you will almost certainly get different results to me. Using the version function and the excellent CPU Info by Ben Tordoff, here are the details of my machine and MATLAB version. versionInfo = ['MATLAB Release R' version('-release')]
versionInfo = 'MATLAB Release R2021a'
cpuinfo()
ans =
Name: 'Intel(R) Core(TM) i7-8650U CPU @ 1.90GHz'
Clock: '2112 MHz'
Cache: '1024 KB'
NumProcessors: 4
OSType: 'Windows'
OSVersion: 'Microsoft Windows 10 Pro'
Your Need for Speed?
MATLAB is faster than it has ever been and it will continue to get faster in the future. This, combined with improved hardware, will help you to answer larger and more complex questions than you ever have before. However, there will always be occasions where we need even more. What MATLAB speed-up techniques do you find useful and what do you wish was faster in MATLAB? Let us know here. Helper functions
function result = floorMyIsPrime(n)
% Function to check if n is prime
function res = floorMyCountPrimes(max_n)
% Count how many primes there are up to and including max_n
function result = uint32MyIsPrime(n)
% Function to check if n is prime
function res = uint32MyCountPrimes(max_n)
% Count how many primes there are up to and including max_n
Copyright 2021 The MathWorks, Inc.
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.