Model-Based Design of a Dicycle
The other day I found this video:
If you watch carefully, you will see around 1:50 that they used Simulink to design their controller.
So for this week's post, I thought it would be interesting to see how we can design a simple planar version of a dicycle in Simulink.
Modeling the plant in SimMechanics
Since this system is not very complex, I could have derived the equations of motion by hands. But even if the equations are simple, it is simpler (and more fun) to model it with SimMechanics.
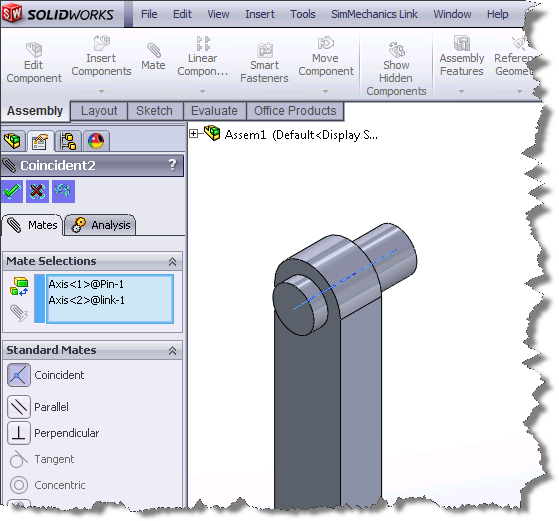
To model this planar dicycle, we need 3 bodies: the ground, a wheel and a center body. The important trick here is the Velocity Driver block constraining the motion of the wheel relative to the ground. Note that, to make the SimMechanics visualization look nicer, I added 2 posts acting as starting and stopping references.

Click on the image to download the model.
Our system has 2 sensors, a gyroscope returning the angle of the body relative to gravity, and an encoder giving the angle of the body relative to the wheel. On the actuator side, the system has 1 motor applying a torque between the wheel and the body.
Testing the plant motion
When developing a plant model, it is important to validate it. To validate the plant, I apply a torque to the actuator and observe if the resulting motion is as expected.

This behaves as expected... but if I don't find a better controller, the passenger will quickly get sick. Let's see how we can design a controller.
Linearizing the plant
Most control techniques I know are based on a linear representation of the system. To obtain this representation, I use Simulink Control Design. I can use the graphical interface or the command-line API. For my model, the command-line version looks like:
mdl = 'Diwheel'; % Set the controller to zero during linearization K = [0 0 0 0]; % Construct linearization input/output io(1) = linio([ mdl '/Ctrl'],1,'in','on') io(2) = linio([ mdl '/Sensors'],1,'out','on') % Linearization sys = linearize(mdl,io);
Designing a controller
Now I will use the Control System Toolbox function lqr to design a state-feedback controller. The code looks like this:
% Get minimal realization [sys U] = minreal(sys); % Design state feedback controller Q = diag([ 100 1 100 1],0); R = 1; [K,S,e] = lqr(sys,Q,R); % Transformation from y to x K = K/sys.C;
All I had to tune are the values on the diagonal of matrix Q to give a priority to each state. You can download the complete initialization script here.
Now if I try to command the vehicle an aggressive trajectory of 1m/s for 10 meters and sudden breaking, I get the following:

Next steps
I will stop here for this post. If I had to implement this controller on a real system, I would have a lot more steps to go through. This would involve adding to the model actuators limits, sensors resolution, discretizing the controller, maybe converting it to fixed-point, etc.
Now it's your turn
Let us know what you think of this control design process by leaving a comment here.







댓글
댓글을 남기려면 링크 를 클릭하여 MathWorks 계정에 로그인하거나 계정을 새로 만드십시오.