Points and Polygons
Ever wanted to know if some points of interest were inside a region? You can answer that if the region is specified as a polygon in MATLAB. The key is the inpolygon function.
Contents
Polygons
Polygons in two dimensions are generally represented in MATLAB with two arrays, locations for the X vertices and Y vertices. There is no need to have the final points in these match the initial points; that is, when arrays as described are used in situations where they are interpreted as polygon vertices, the polygon is automatically closed.
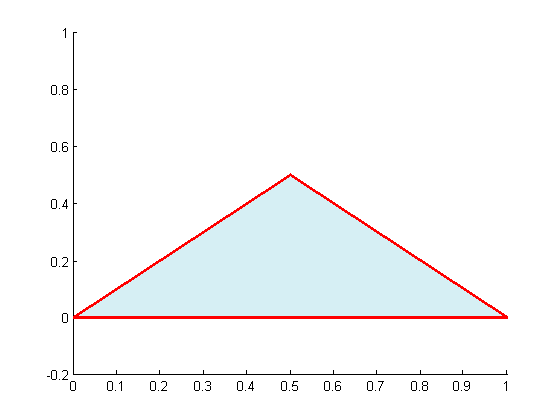
Let's define a very simple polygon to start.
X = [0 0.5 1]'; Y = [0 0.5 0]';
And look at it.
patch(X,Y, [0.2, 0.7, 0.8], 'edgecolor','r',... 'facealpha', 0.2, 'linewidth',2); axis([0 1 -0.2 1])
Some Points of Interest
Let's create some points of interest now. Some inside, some outside, and some on the boundary.
xin = [0.3 0.75 0.82]'; yin = [0.25 0.1, 0.05]'; xout = [0.3 0.75 0.82]'; yout = [-0.15 0.6, 0.3]'; xedge = [0.3 0.75 0.82]'; yedge = [0.3 0.25, 0.18]'; hold all plot(xin, yin, 'g*', 'markersize',5) plot(xout, yout, 'mx', 'markersize',9) plot(xedge, yedge, 'bd', 'markersize',7) hold off

Test the Points with the Polygon
[inIN onIN] = inpolygon(xin,yin, X, Y)
inIN =
1
1
1
onIN =
0
0
0
[inOUT onOUT] = inpolygon(xout,yout, X, Y)
inOUT =
0
0
0
onOUT =
0
0
0
[inEDGE onEDGE] = inpolygon(xedge,yedge, X, Y)
inEDGE =
1
1
1
onEDGE =
1
1
1
Multiply-connected Polygon
Here's an example from the help for inpolygon, with a square containing a square hole. The outer loop is counterclockwise, the inner clockwise.
xv = [0 3 3 0 0 NaN 1 1 2 2 1]; yv = [0 0 3 3 0 NaN 1 2 2 1 1]; x = rand(1000,1)*3; y = rand(1000,1)*3; in = inpolygon(x,y,xv,yv); plot(xv,yv,x(in),y(in),'.r',x(~in),y(~in),'.b')

Do You Work with Points and Polygons?
Have you used inpolygon? I'd love to hear the contexts of the problems you solve with it.
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.