INPOLYHEDRON
Sean's pick this week is inpolyhedron by Sven.
Polygons, Polyhedra and Convexity
It's often useful to know if a point is inside of a polygon (two dimensions) and sometimes if a point is inside of a polyhedron (three dimensions). For two dimensions, MATLAB ships with inpolygon, a nice function to handle this. However, this same operation in three dimensions becomes more complicated. It is simplified if the object is convex. In this case, the vertices can be represented as a set of constraints and we can apply these constraints to the points to test whether they are inside or not. Matt J does this in his vert2lcon function (The runner-up, who will also get some MathWorks swag, for this week's post!).
But what about when the polydehron is not necessarily convex? Now we no longer have this luxury and have to resort to more complex algorithms.
Fortunately, Sven has done the work for us!
Let's use Paul's three dimensional L-Shaped Membrane.
% Load shellVertices, shellfaces from Paul's Blog: load PaulsMembrane.mat % Draw the membrane: patch('Vertices',shellVertices,... 'Faces',shellFaces,... 'FaceColor','r'); axis tight view(-51,24)
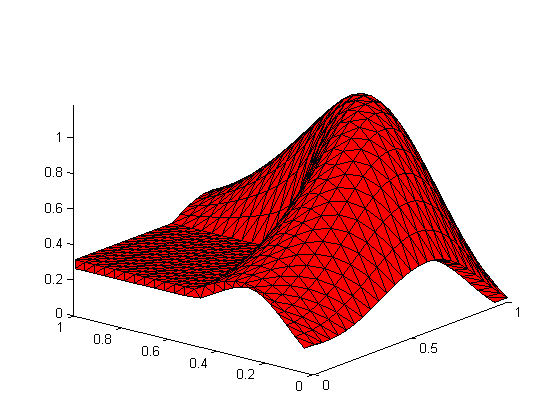
Add 10000 random points to it
pts = rand([10000,3]); %Generate a random 10000pts hold on; plot3(pts(:,1),pts(:,2),pts(:,3),'b*'); %add points to plot
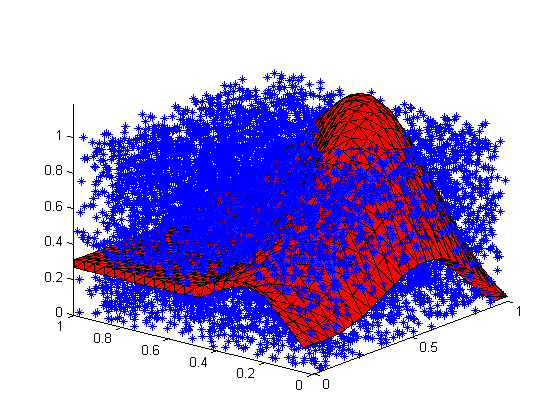
Find the points in the polyhedron
in = inpolyhedron(shellFaces,shellVertices,pts,'FlipNormals',true); delete(hLine); %clean up plot3(pts(in,1),pts(in,2),pts(in,3),'b*'); %add points to plot set(hPatch,'FaceAlpha',0.3,... 'EdgeColor','none'); %make the points inside visible

Woohoo!
Comments
In addition to everything you saw here, there is also excellent help and many options built into inpolyhedron. Give it a try and let us know what you think here or leave a comment for Sven.
- Category:
- Picks
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building






Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.