This week I am happy to welcome guest blogger Zack Peters to describe how he implemented the simulation of a ski jump, similar to the Men's large Hill Individual event of the PyeongChang Winter Olympics starting this Friday.

Introduction

In case you are not familiar with the Olympic Ski Jump competition, let's start with a video explaining what it involves:

In order to maintain consistency and safety for the jumpers, there are a set of thorough standards written by the International Ski Federation (FIS) regarding the shape/profile of the ski jump ramp. Here is a picture taken from the Standards for the Constructions of Jumping Hills document showing all the specifications of the ramp (typically called In-run) and landing area. In this document, you can find all the numbers and equations defining the shape shown in this picture:

The Implementation

As you can imagine, this system could be modeled in many ways. One option would have been to use a conditionally enabled subsystem for each phase of the jump, in a way similar to how we simulated the pole vault competition in the previous summer olympics. Another option would have been to use the new Simulink States inside Stateflow, like we used to simulate a box jumping on a table a few months ago.

For this post, I decided to implement the ski jump dynamics using the Simscape language. I thought it would be a good application to utilize some of the new features available in R2017b like modecharts and and Simscape Functions

Some Symbolic Pre-Work

First, let's draw the free body diagram of a body moving along the In-run:

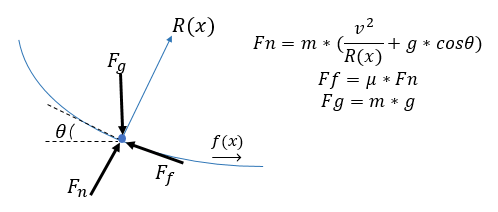
As mentioned above, the FIS standard gives a great description of the hill profile (a relationship in the form y=f(x)). From there I need the slope (theta) and the radius of curvature (R) to compute the normal force (Fn). This can be obtained by differentiating the hill profile twice. To help with that, I used the Symbolic Math Toolbox. In case you were not aware, the Symbolic Math Toolbox is now well integrated into the MATLAB Desktop through the MATLAB live script technology.

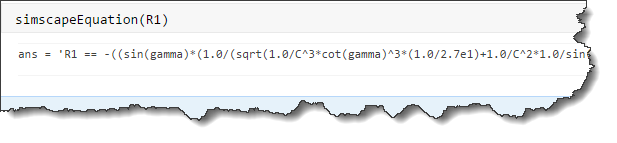
To bring the final result into Simscape language, I used the simscapeEquation function, also from the Symbolic Math Toolbox.

Modechart

In my Simscape component, I defined a modechart with 3 modes: In-run, airborne and landing:

and I defined the conditions at which the system switches from one mode to the next:

Simscape Functions

When looking at the above code, you might wonder what are those functions like "jumpPkg.jump.slope" and other similar. Those are Simscape Functions, introduced in R2017b.

These allow for improved readability of the component and reuse of utility components. I packaged these up in a directory structure that would break up separate equations for the In-run and the landing area, allowing me to give the equations the same name, but a different path. Here is what my package looks like:

Inside those functions, I used the equations derived using the Symbolic Math Toolbox. Here is an example for the slope of the In-run.

As you can see, the In-run has 3 separate sections implemented using an If/Else statement in the Simscape Function.

Here is an animation of the simulation results:

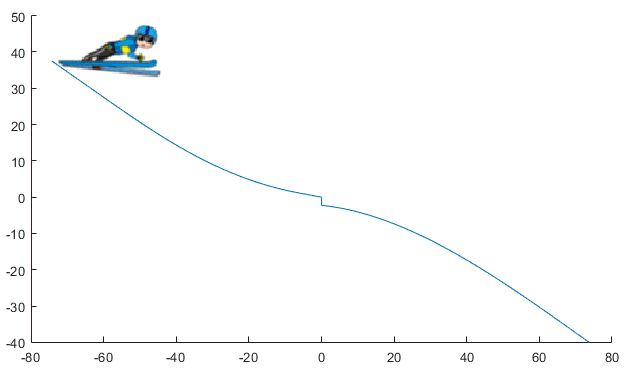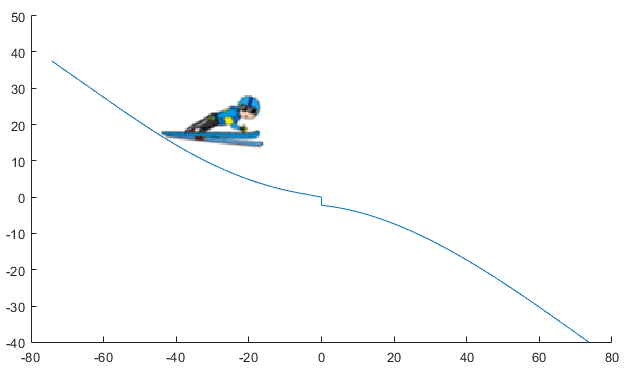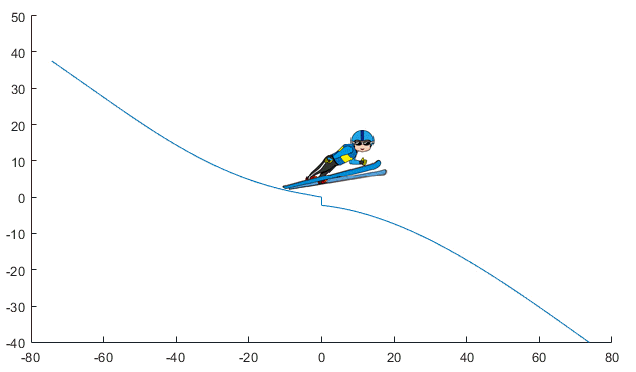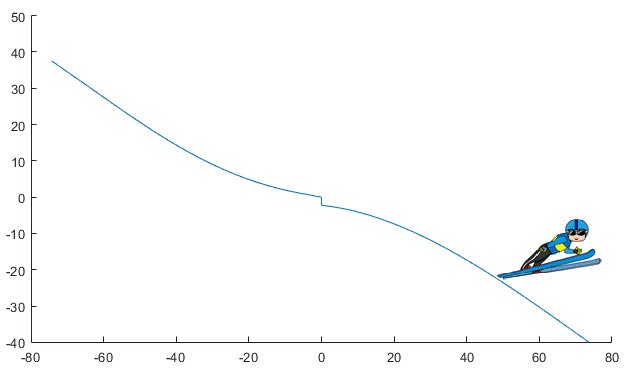
Now it's your turn

Anybody interested in adding more fidelity to our jumper model? Are there other Olympic sports you would be interested to simulate? Let us know in the comments below.