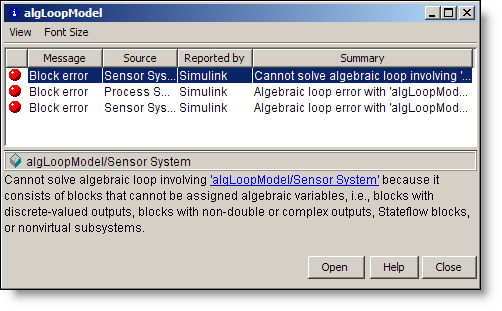
A few days ago I had to debug a very large model generating an error similar to the following:

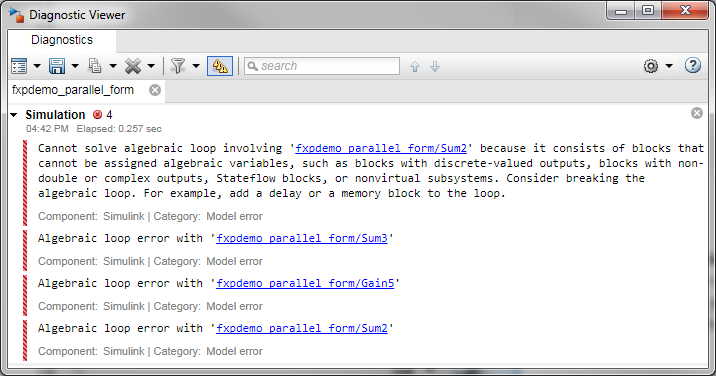
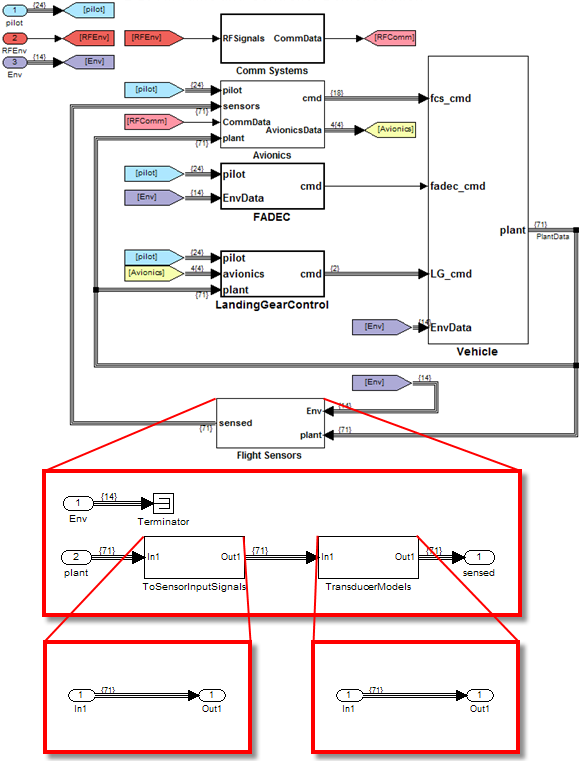
In my case, the loop involved more than a hundred blocks and signals spread everywhere in the model and combined in buses, which was making it complex to analyze.

ashow (And why you don't need it anymore!)

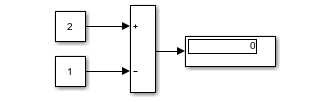
For many years, I have been using the ashow function to highlight algebraic loops. Here is an example of how it works for a simple model:

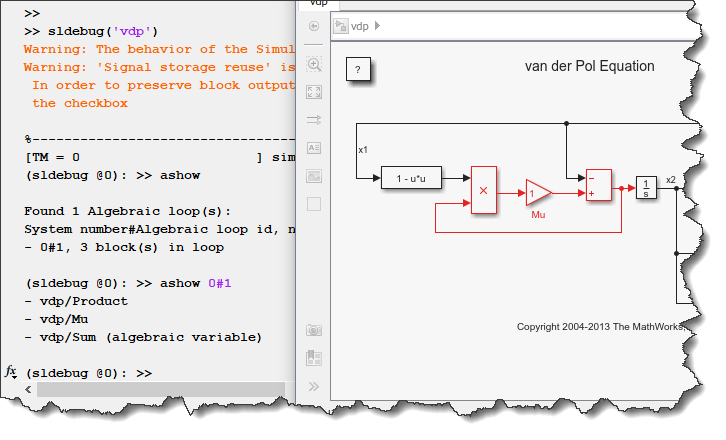
However, in addition to a few usability challenges, one major difficulty with ashow is that it can only highlight a subset of algebraic loops - and, of course, it cannot highlight the one I needed to solve.

The limitation affecting me was that the algebraic loop was made of fixed-point signals. This led to a sort of chicken-and-egg problem. For ashow to work, it needs the model to be compiled. But since the loop is made of fixed-point signals, the Simulink engine knows that it cannot solve the loop, and errors out during model compilation, making it impossible to use ashow.

That's when I remembered a relatively new function that I tend to forget: Simulink.BlockDiagram.getAlgebraicLoops

Simulink.BlockDiagram.getAlgebraicLoops

If you read the documentation page on algebraic Loops attentively, you might have noticed that Simulink now offers the function Simulink.BlockDiagram.getAlgebraicLoops, a more modern and powerful way to highlight algebraic loops.

For the same example as above, here is what it looks like:

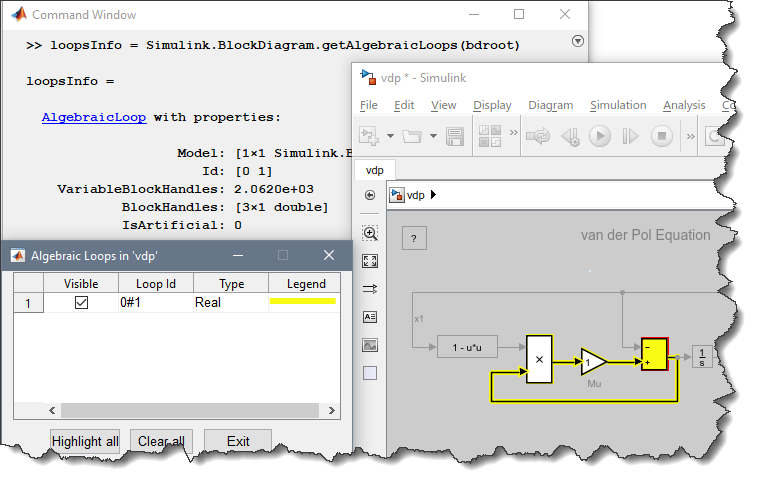
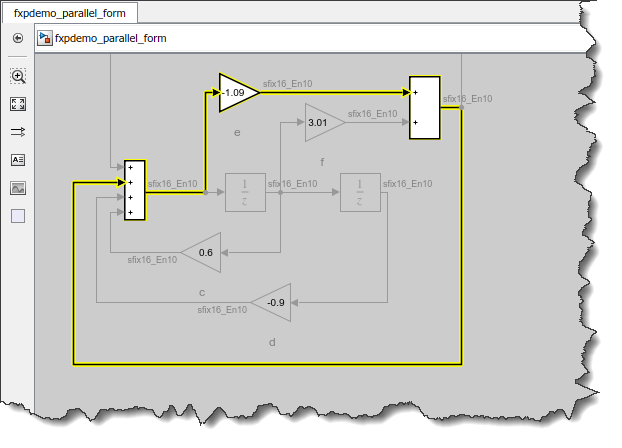
This function was introduced in R2015a, and in R2017b it was enhanced to be able to find and highlight more types of algebraic loops. In my case, it allowed me to highlight a loop made of fixed-point signals. Seeing the loop allowed me to figure out the best place to introduce a delay and break the loop.

A few things to note:

• The block highlighted in red is what we call the algebraic variable. Introducing a delay at the output of this block is probably a good first thing to try to remove the algebraic loop (Unless the loop is continuous, as explained in this post).
• If we detect that the loop is artificial, it will be highlighted with a dashed line, meaning that you should fix it using the Minimize Algebraic Loop feature of Atomic Subsystem or Model Reference.
• Simulink.BlockDiagram.getAlgebraicLoops also returns an output object with properties of the loops in the model, including handles to the blocks involved, which you can use at your convenience.

Here is an example of a fixed-point model with an algebraic loop highlighted:

Now it's your turn

Are you struggling with algebraic loops? Does using Simulink.BlockDiagram.getAlgebraicLoops help you understanding them better? Let us know in the comments below.