What’s the reaction when we touch?
Greg's pick this week is Rolling Ball on Plane by Janne Salomäki.
Janne put together a nice example of modeling the interaction of a ball contacting a plane, rolling on the plane, and then falling off the plane.
Janne uses SimMechanics to model the geometry and motion of the ball and the plane. And then applies C-code S-Function to model the interaction between the ball and the plane. Contact modeling isn’t something SimMechanics can do, so I’m excited to see an example that shows the basic concept. I also saw an opportunity to compare using C-code and MATLAB Code to solve this particular problem.
Contents
What is SimMechanics?
SimMechanics enables six degree of freedom (6DOF) modeling of rigid bodies in Simulink. A nice benefit is it comes with an animation feature where you can visualize the motion of the bodies. Bodies are defined in terms of mass, inertia tensor, and location for the center of mass. Connections to other bodies are defined by coordinate systems applied to the body, and placing constraints on the type of motion permitted between two coordinate systems. For example, a revolute joint only has one degree of freedom, while a gimbal joint has three degrees of freedom.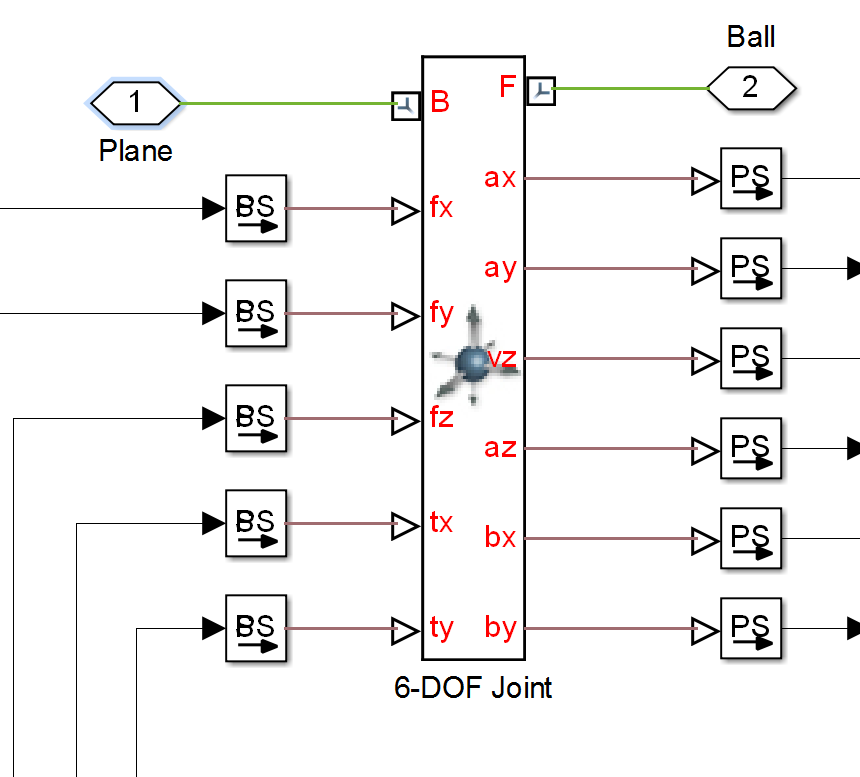
In this particular case, the joint between the ball and the plane has six degrees of freedom, which means there is no restriction on the relative motion between these two bodies. Using this joint enables measurement and actuation of the relative motions between the two bodies, which is essential for modeling the contact interaction.
What is an S-function?
An S-Function is a “system function”. It is a way to create customized blocks in Simulink that can extend its functionality. People use S-Functions to for all sorts of capabilities:- Interface Simulink models with other software running on your computer
- Compile an optimized block algorithm to improve performance
- Protect intellectual property
- Integrate existing code into a Simulink model
Are there other ways to do this?
There are other ways to develop the interaction model. You could of course use basic Simulink blocks, and develop the equations using Add blocks, Gain blocks, etc. Another option is to write the interaction as MATLAB-Code in the MATLAB Function block. This would enable you to test the algorithm in the flexible MATLAB environment. The MATLAB Function block is not designed to support mathematical integration. So it is often best to pass out the derivatives of the states as outputs, route them through an integrator block, and pass the result back as inputs to the MATLAB Function block.
How do they compare?
|
C-code S-Function |
MATLAB Function |
MATLAB Function (Debugging Disabled) |
|---|---|---|
|
2.15 sec |
2.67 sec |
2.30 sec |
|
~ |
+24% |
+6.8% |
MATLAB Debugging Disabled
 Leaving the debugging on certainly provides for a much bigger performance hit, but it also means you can step through the
code using the MATLAB Debugger. This is a bit more difficult to do when you need to debug the C-code S-Function.
I’ll leave it to you to decide if the convenience of the MATLAB Code is worth the hit in performance.
Leaving the debugging on certainly provides for a much bigger performance hit, but it also means you can step through the
code using the MATLAB Debugger. This is a bit more difficult to do when you need to debug the C-code S-Function.
I’ll leave it to you to decide if the convenience of the MATLAB Code is worth the hit in performance.
What do I like about this entry?
First, it is a neat, clean, and clear model. Both the model and the code for the S-function are done in a nice straight forward manner. I like the use of the macros in the C-code S-function to make the code easier to read by hiding some of the weird API language. What I find so fascinating is that SimMechanics handles all of the appropriate coordinate transformations, so the algorithm for the contact model is relatively simple without a lot of math to figure out the body relationships. I realize this approach might not scale well to a more general implementation of contact modeling, but I think it’s a beautiful and creative example of investigating rigid body dynamics.Do you need contact modeling in SimMechanics?
Let us know how you would use it. Do you create S-Functions? What’s one thing you like about them? What’s one thing you dislike about them? You can leave your comments here. Published with MATLAB® 8.4
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building






Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.