Round-off Error
Loren recently posted a simple example of how single-threaded computations might produce different results from multi-threaded computations. The cause is floating-point round off, and most people are surprised to learn that the "different" results actually agree! In this post, I want to explore this same example in Simulink.
Order of Operations is Important
Loren’s example shows that the answer you get from the following equation depends on the order that you perform the operations:
1e-16 + 1e-16 + 1e30 - 1e30
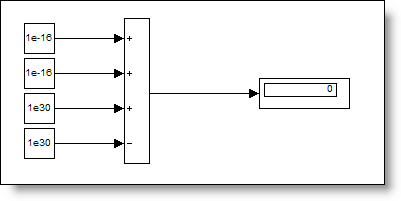
Here is the same equation expressed in Simulink blocks. The model doesn’t explicitly specify the order of operations, so they are done from first to last input (top to bottom, ie ((1e-16 + 1e-16) + 1e30) - 1e30).
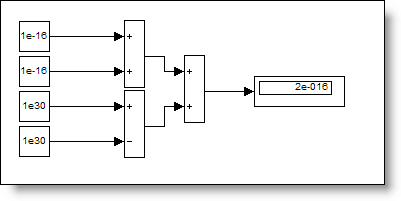
Here is the same equation with a different parenthetical grouping, where the inputs to each operator are signals of the same magnitude.
(1e-16 + 1e-16) + (1e30 - 1e30)
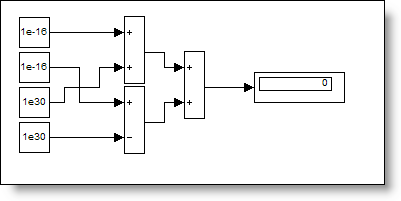
In another grouping, the inputs to the operators have very different magnitudes.
(1e-16 + 1e30) + (1e-16 - 1e30)
I like these examples because they show how floating point round off affects the result. An important aspect of these calculations to consider is the spacing between floating-point numbers of a certain magnitude. The EPS command gives you the difference between a number and the next floating-point precision number. What is EPS for 1e30?
>> eps(1e30)
ans =
1.4074e+014
Considering that the spacing of floating-point numbers around 1e30 is MUCH larger than 1e-16, you can why there is sensitivity to the order of these operations. For any normal floating-point number X, you can expect no difference in the result if you add less than half EPS(X).
>> 1e30 + 7e13 == 1e30
ans =
1
>> 1e30 + 8e13 == 1e30
ans =
0
How could this really affect me?
Imagine a model where precision in the results is a critical consideration. Choices made about the units of parameters, and the order of operations could have an impact on precision of the calculation, especially if working with a more compact number representation like single precision floating-point.
Now it’s your turn
Have you ever run into a strange result only to find out it was within the bound of floating-point error? Share your experience with us in a comment here.
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building




댓글
댓글을 남기려면 링크 를 클릭하여 MathWorks 계정에 로그인하거나 계정을 새로 만드십시오.