After finding the launch date of the mission and putting together a simulation of the spacecraft trajectory, it's time to see how we can optimize this trajectory.

Let's bring him home!

Optimizing the Trajectory

First I have to confess that I am not expert in optimization. That being said, I was pretty impressed by how easy it was to get it to work using our tools.

Since this problem is actual rocket science and I am not a rocket scientist, I decided to not begin with the full Rich Purnell Maneuver. Instead I started with a problem of more reasonable scale: the original planned trajectory for the Ares 3 mission, which was to get to Mars in 124 days, and come back to Earth exactly one year after the launch date.

The simulation I created, which I showed last week, is set up so that it takes as input a vector of thrust angles, and logs the position of the ship.

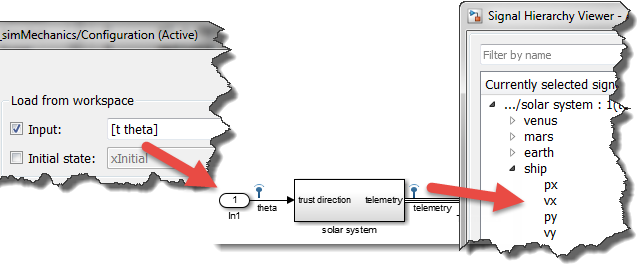
To determine how good the trajectory is, I have two criteria: I want to be at a specific position and velocity relative to Mars on day 124, and at a specific position and velocity relative to Earth on day 365. So my cost function code looks like:

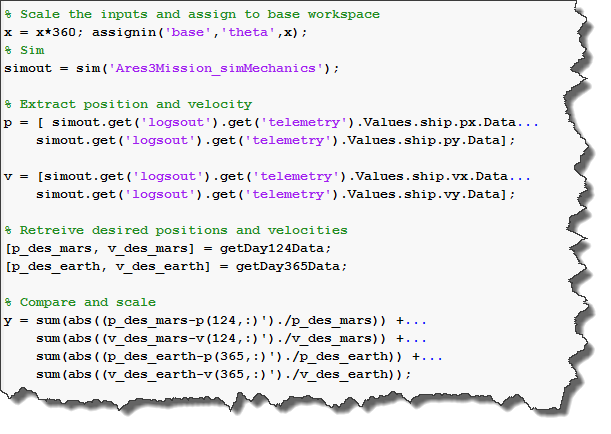
Notice that I decided to scale the inputs and outputs so that they are in the amplitude range of 1. Someone once told me that default settings for optimization algorithms work better using that scale.

Then all I need to do is pass this cost function to fmincon, from the Optimization Toolbox. I took advantage of the Fast Restart feature to speed up my workflow; for this specific model the initialization takes more time than the simulation itself, so Fast Restart significantly reduces the processing time it takes for the optimization to converge:

After about 10 minutes, I marvelously obtained a nice trajectory that does the fly-by Mars on day 124 and comes back to Earth after a year:

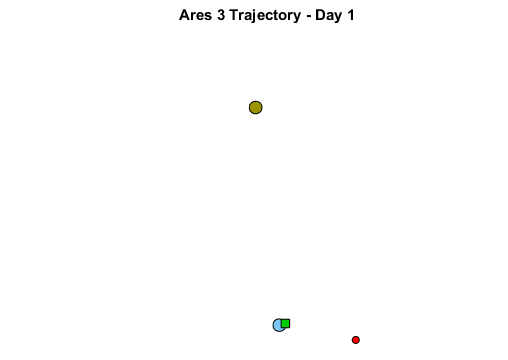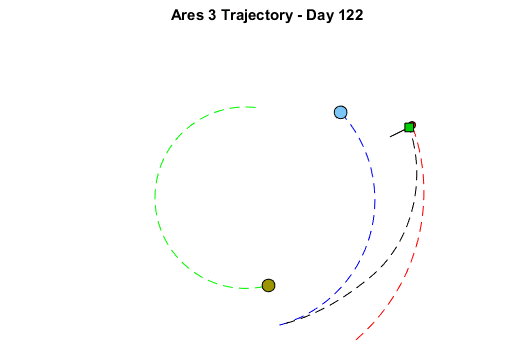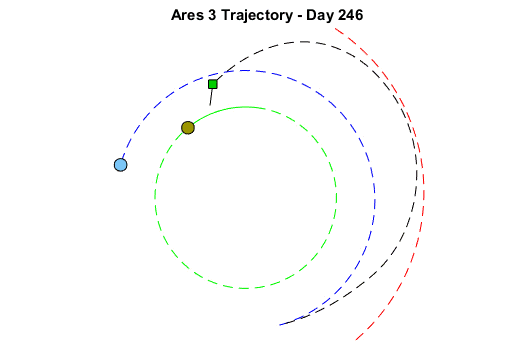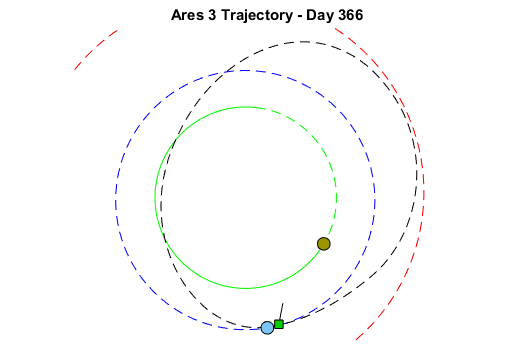
Now it's your turn

If you are interested, you can download the whole optimization problem here. I am still very curious... if someone can simulate the full Rich Purnell Maneuver, I will keep my promise of providing nice MathWorks swag!