The Simulink Curling Simulator… we did it!
After I published my post on simulating figure skating in Simulink, my colleague Corey Lagunowich and I discussed what other Olympic sports would be fun to model in Simulink. We settled on one of his favorites: curling.
We got completely hooked on this challenge and before we knew it, we had a fully detailed simulator allowing you to play complete curling games!
We thought you might be interested, so we decided to share our Curling Simulator on MATLAB Central File Exchange. In this post we describe how we modeled the dynamics of the moving stones in Simulink.
The Big Picture
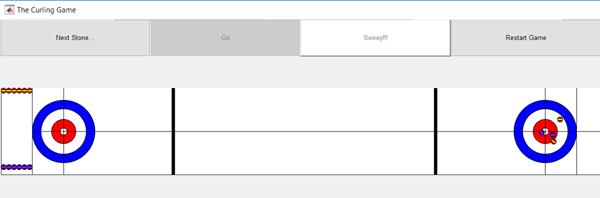
Our submission primarily consists of a MATLAB App and a Simulink model.
In the App, you decide where you want to aim, how fast you want to throw the stone, and what spin you want to put on it. When you click the Go button, the MATLAB App starts the Simulink model using the sim command. While it runs, the Simulink model uses a Level-2 MATLAB S-function to redraw the position and orientation of every stone in play.
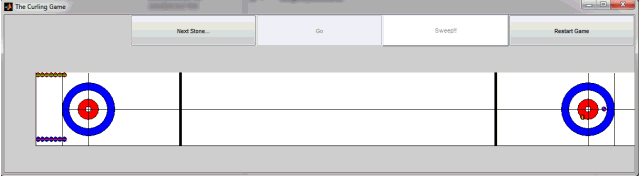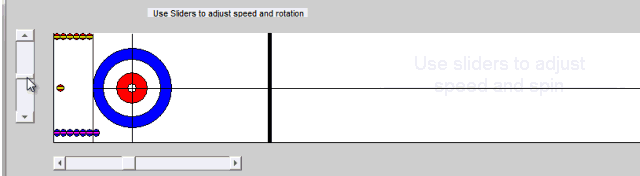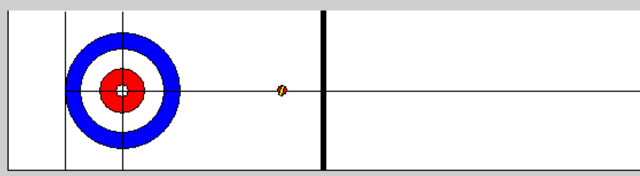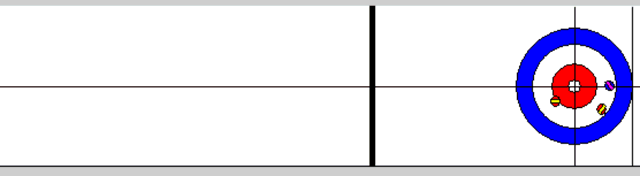
In this post we are not going into the details of the interactions between the App and the model… maybe in a future post.
The Simulink implementation of the game dynamics is centered around one Second-Order Integrator block. The size of the signal is proportional to the number of stones on the ice.

Inside the Curling Model subsystem, we have two main components working in parallel: a contact model and a friction model.
The Friction Model
When he started developing a model for the friction, Corey quickly discovered that there is a lot of interest in the scientific community in curling. Understanding the movement of the stones on the ice has important implications in the field of tribology.
Based on what he learned, Corey parameterized lookup tables to calculate the force exerted by friction on the stone as a function of the stone's speed, angular velocity and the friction coefficient (which is function of how much you sweep…. Be sure you try the sweep button in the App!).

There are a lot of things about the behavior of spinning objects on ice that are counter-intuitive at first. For example, the faster you spin a curling stone, the less it actually curls. But if you don’t spin the stone at all, it erratically zig-zags down the ice. Researchers have yet to come to a consensus on the exact mechanisms for all of this behavior (you can read more about it in this article on National Geographics News or this article on phys.org).
Let's see the behavior in our simulator of two consecutive stones, one with low spin, and one with high spin

Watching a simulated stone curl realistically across our virtual ice was pretty exciting, but we couldn’t stop there. We expanded the model to simulate all 16 regulation stones at once. Doing that was actually pretty easy… all we had to do was drop the friction model for one stone into a For Each Subsystem.
The Contact Model
But what about simulating collisions? The contact model, we first computes the distance between each pair of stones. If we detect a contact, we compute new initial velocities and reset the Second-Order Integrator (This logic is similar to the bouncing ball demo).
To manage all the possible combinations of stones hitting each other, I used two nested For Iterator Subsystems (not to be confused with the For Each Subsystem) and an Enabled Subsystem. That way, the model computes new velocities only for the pair of stones in contact.

To compute the transfer of momentum, I found the perfect example in my Meriam and Kraige Engineering Mechanics Dynamics book I had bought during my first undergrad semester.
In the App, I was pretty impressed when I first saw the stones colliding together:

Now it’s your turn
Head on over to MATLAB Central, download the Curling Simulator, and use Simulink to hone your curling strategy! The 2018 Olympic qualifiers start sooner than you think!
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building






Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.