Seth on Simulink

October 9th, 2008

I haven’t seen much activity on the Metronome Synchronization Challenge, so I want to provide a peak at the basis for my solution.  I took the approach of modeling a pendulum, and then linking its dynamics to the dynamics of a cart.  The challenge is choosing the right coordinate systems to assign to each of these bodies, even though they move together.

The Pendulum

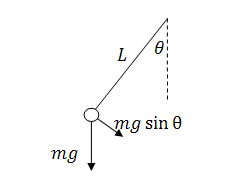
If the pendulum was all by itself, we could describe its motion by modeling the angle, , as it deflects from vertical.  The only force on the pendulum bob is gravity.  Because the pendulum is constrained to rotation about the pivot point, we only need the component of gravity in pendulum frame of reference.

If we incorporate the motion of the cart, we find the linking of the acceleration of the cart to the acceleration of the pendulum bob.  If the cart is accelerating, the reference frame of the pendulum accelerates, and this means that the pendulum will experience an opposite force/acceleration.

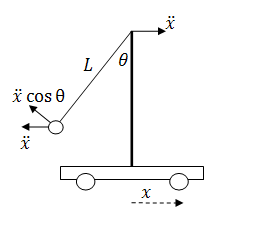
Combining these two ideas in the  frame centered on the pendulum pivot, we can write the pendulum equation of motion.

Momentum in the system

To understand the acceleration of the cart, I want to look at the change in the  component of the momentum.  Here are some definitions:

Length of the pendulum:        
Mass of the pendulum bob: 
Mass of the cart:                      

The momentum of the pendulum bob in the  direction

The momentum of the cart is

The friction of the cart on the surface is the only resistance I want to model in the system, and we can describe this force as proportional to the velocity, . This represents of the change of momentum.

Combine these terms to describe the momentum in the  direction.

Up to this point, I have looked at the problem of a single pendulum on a cart.  Adding another pendulum is just another momentum term, and to keep track of the pendulums we will introduce  and  .

Taking the derivative of this equation gives us the acceleration of the cart:

System Equations

This equation for the cart, along with the dynamics of the pendulum provides the equations of motion for the system.  Rewriting these as the highest order derivatives gives us something we can create in Simulink.

Are you up to the challenge?

Can you modify the model I provided in my last post to implement these equations?  Post your solution by October 15^th to the File Exchange with the keyword metronome.

09:00 UTC | Posted in Challenge, Modeling, ODEs | Permalink |

You can follow any responses to this entry through the RSS 2.0 feed. You can skip to the end and leave a response. Pinging is currently not allowed.

3 Responses to “Challenge: Metronome and Cart Equations of Motion”

1. ABindemann replied on October 9th, 2008 at 11:30 UTC :
   

   Hmmm, is a simple pendulum an appropriate mechanical model for a metronome? What you’ve modeled is a vertically hanging, gravity stabilized pendulum rather than a spring stabilized inverted pendulum. Based on your approach you should “flipud” your metronome scope ;-)

2. Seth replied on October 10th, 2008 at 14:08 UTC :
   

   @ABindermann - you are right… I should flip the metronome scope. Is this an appropriate mechanical model for a metronome? I have played around with a version using an inverted representation and a spring to stabilize it, and I didn’t see much difference in the behavior. The other experiment I tried was adding friction to the metronome and an energy reserve to kick the pendulum back. I found all of this made things more complicated without much benefit.

   This is the metronome I was thinking about as I approached the problem:

   

3. Thomas Steffen replied on October 14th, 2008 at 13:05 UTC :
   

   I have uploaded a file, but it will take a while to appear. I think the synchronisation will not work with a purely linear model, because that will produce several resonance frequencies. I modelled the driving force of the metronome, and that did the trick.

Leave a Reply

<pre class="code">
a = magic(3);
sum(a)
</pre>

These postings are the author's and don't necessarily represent the opinions of The MathWorks.