Challenge: Metronome Synchronization
My good friend Doug, formerly of Pick of the Week fame, sent me an e-mail last week with the subject “Model this.” The message contained nothing more than a link to a video. Doug started a new video blog, and for this reason, I have decided to incorporate some video into this post.
What is happening?
The video shows five metronomes sitting on a board, and when they start, the timing is initially out of phase. The board is placed on top of empty soda cans on their side, allowing the board to slide back and forth with very little friction. The board couples the dynamics of the metronomes and, in time, their phases synchronize. The synchronization of periodic systems is a fascinating concept, and fun to watch. This effect was first observed by Huygens in the 17th century. You can find many related videos on YouTube, like this presentation of metronomes with different frequencies and this experiment with five metronomes.
The Challenge
In honor of Doug’s latest venture, here is a challenge:
Can you model this in Simulink?
You can take many different approaches in modeling
this system. I hope to see implementations using base blocks as well as
SimMechanics.
Hints
To get you started, I have built a simple pendulum and cart model. Download:
metronome.mdl
metronomeAnimation.m
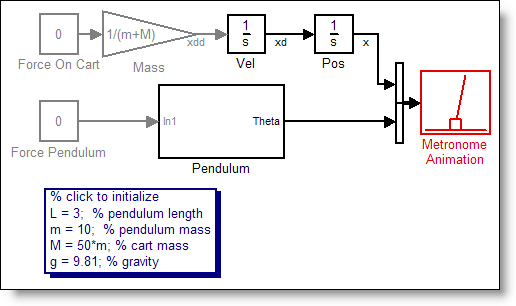
The solution I have explored only shows synchronization when the pendulum angle of deflection is small. I recommend initial deflections of around pi/8 or smaller for the angle of the pendulum.
I have even built a “metronome scope” which will display a crude pendulum given the angle of deflection in radians.

How to submit a solution
Post your solution by October 15th to the File Exchange with the keyword metronome. I will give out some prizes like T-shirts and other stuff I find in the MATLAB Central prize closet. Please post a comment if you have submitted a model to the file exchange, or if you have questions about the challenge. Good luck!
- Category:
- Challenge,
- Modeling,
- Simulation
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.