From Symbolic to Simulink
I am recently visited the MathWorks Japan office and learned about interesting work done by my colleague Hitoshi Takeshita.

In his MATLAB Central submission Euler–Lagrange equation, Hitoshi shows how the Symbolic Math Toolbox can be used to easily obtain the equations of motion of a system by simply defining the energies involved. Once the equations of motion are obtained, he then uses the code generation capability of the Symbolic Math Toolbox to create a Simscape component and simulate the system in Simulink.
I had never used this workflow before, but it can be very useful in applications like plant modeling and for engineering students learning systems dynamics.
Let's look at an example using a double mass-spring system:
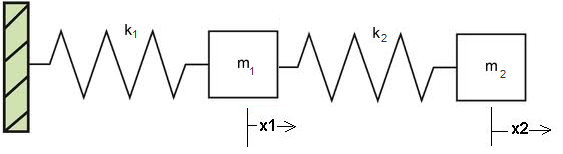
Modeling a dynamic system in MuPAD
MuPAD is the engine of the Symbolic Math Toolbox. If you never used it, I recommend going through the Getting Started section of the documentation, or read some of the posts in the Symbolic category of Loren's blog.
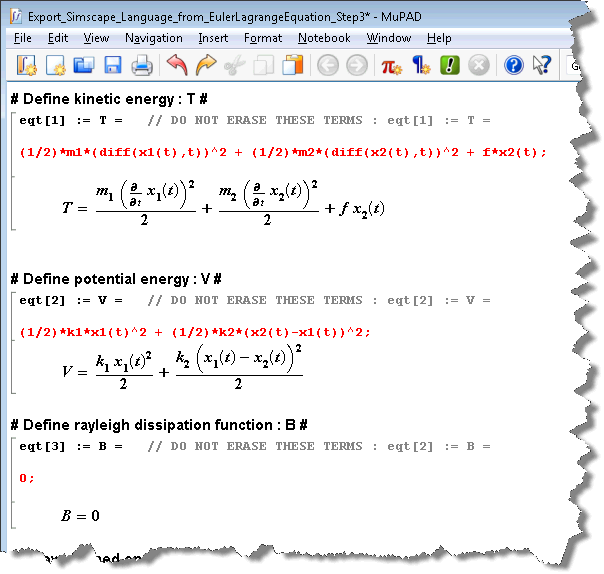
In the MuPAD Notebook provided by Hitoshi, all you need to do is define the kinetic energy, potential energy and dissipation function:
The rest of the notebook implements the Euler Lagrange equation:
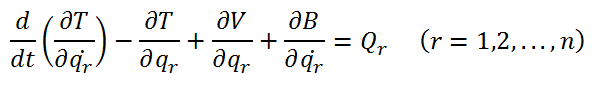
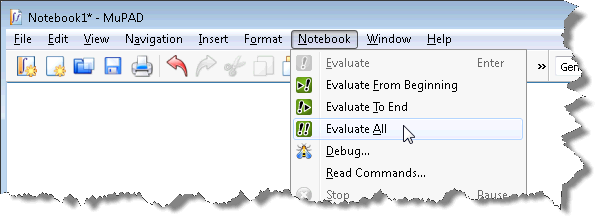
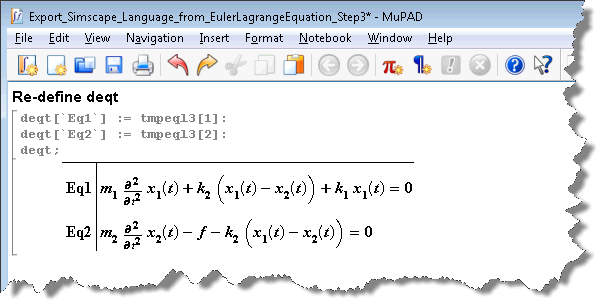
So all you need to do is evaluate the notebook:
and you should obtain the equations of motion of the system:
From MuPAD to Simulink
Now that we have the equations of motion of the system, we want to bring them into Simulink. For that, we use the Simscape language.
In the MuPAD notebook, it is possible to generate Simscape equations using the generate function:

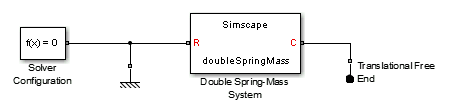
We can then copy and paste this code in the equations section of a Simscape file. We let you write the rest of the Simscape so you can integrate the equations the way you want. In my case, I created a component with two ports, keeping the motion of the middle mass internal to my component. I also modified the names of a few variables auto-generated by MuPAD:

I can then execute ssc_build on this file and obtain a block that I can use in Simulink:
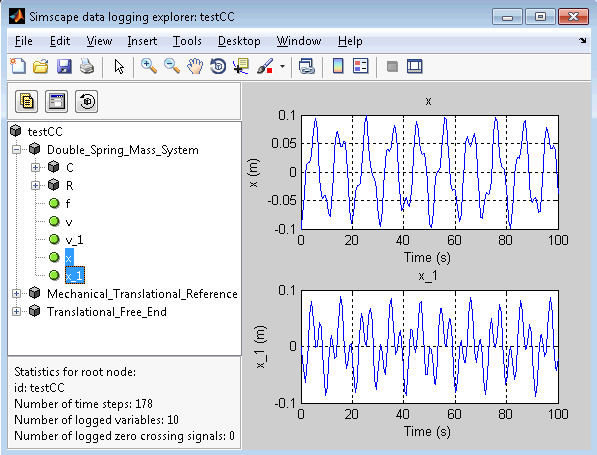
Using the Simscape Simulation Results Explorer I can see that the two masses are moving as expected.
Now it's your turn
Using this method for a simple system like this one is probably not the most efficient way to quickly get a working simulation.
However, I think this method can be very interesting for plant modelers analyzing complex systems and for engineering students trying to get familiar with Lagrange mechanics and equations of motion.
Do you need to combine symbolic manipulations and Simulink? Is the approach highlighted here relevant for your applications? Let us know what you think by leaving a comment here.
- Category:
- Modeling,
- ODEs,
- Physical Modeling
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.