Win Olympic Gold with SimMechanics: Modeling Figure Skating and Angular Momentum
With the XXII Winter Olympics starting this week, I thought we should take the time to model something from the games! So lets look at how conservation of angular momentum is important in figure skating.
The problem
Some time ago a user asked me to illustrate the conservation of angular momentum in SimMechanics. In my opinion, there is no better application to illustrate this phenomenon then a figure skater spinning. As you are probably aware, when a figure skater spins, bringing her arms closer or further from her body changes the speed at which she spins.

OpenStax College - Angular Momentum and Its Conservation - http://cnx.org/content/m42182/1.5/
It's pretty simple, the angular momentum, which is the product of the angular velocity and the moment of inertia remains constant. If one increases, the other must decrease.
A Simple SimMechanics Version
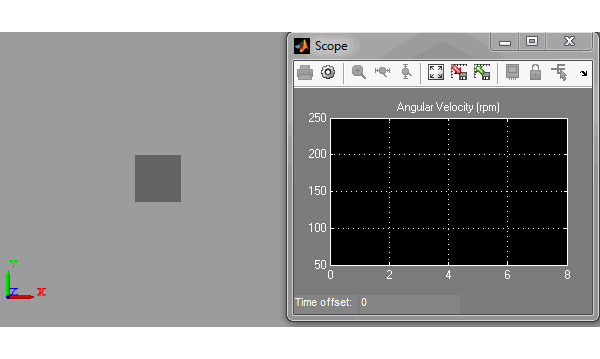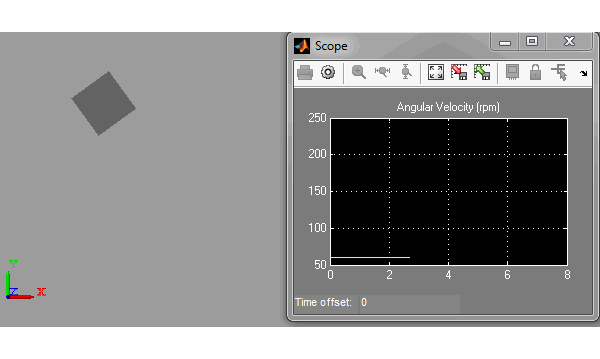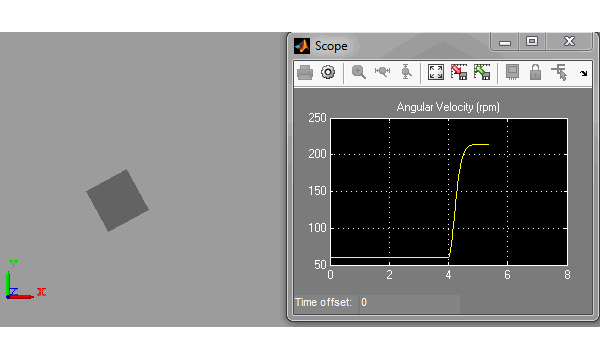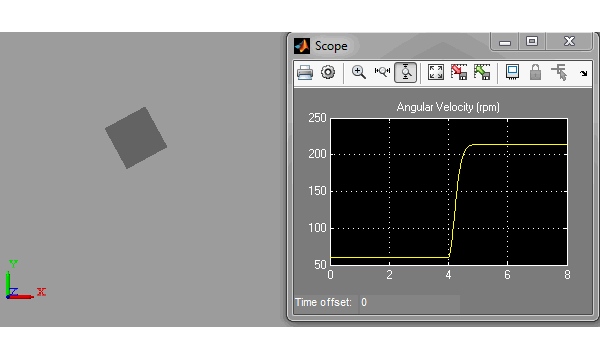
Before implementing a complete figure skater, I thought it would be a good idea to begin by the simplest model highlighting conversation of angular momentum. Here is what it looks like:
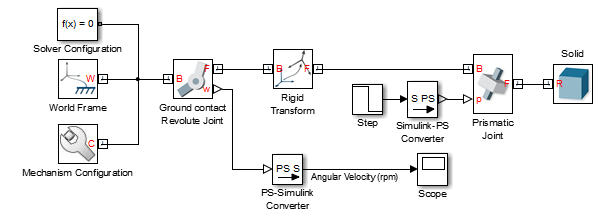
As you can see, I use a a prismatic joint to change the distance of a body from the center of rotation around a Revolute joint. When looking at the results, we can see that the rotation speed increases when the body comes closer to the center.
The Spinning Skater
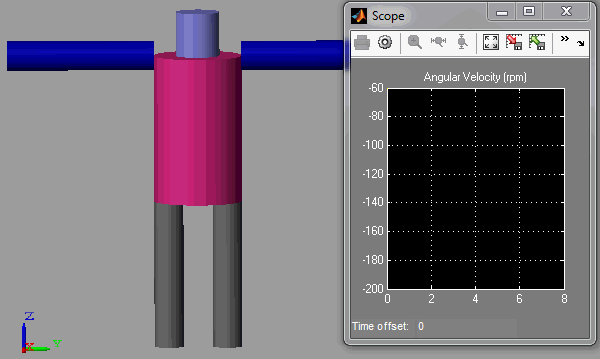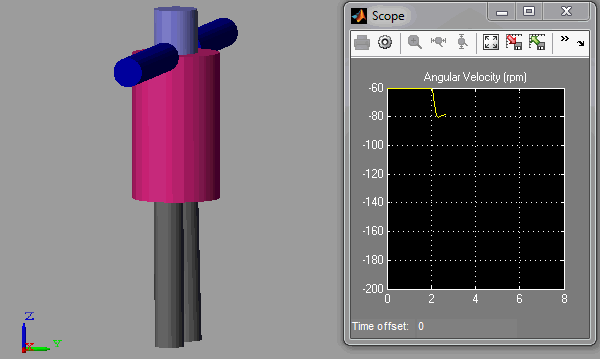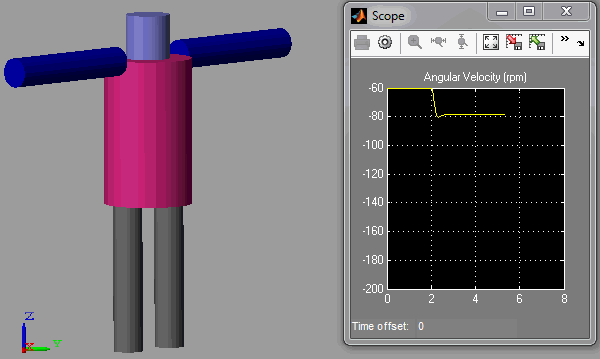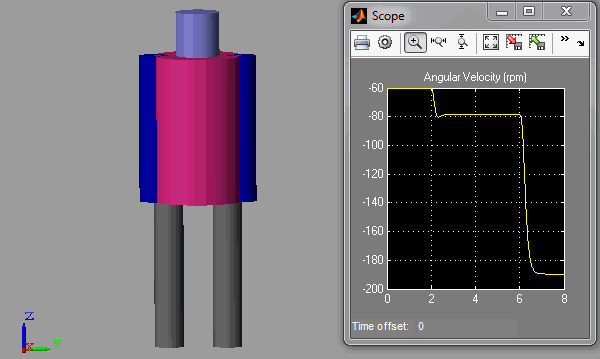
To make my simulation closer to what you will see during the Olympics, I modeled a simple skater using 2 cylinders for the legs, 1 large cylinder for the body, and two cylinders for the arms. I attached the legs and arms to the body using revolute joints. To apply the spinning motion, I attach one leg to the ground using a revolute joint, and I simply give this revolute an initial angular velocity.
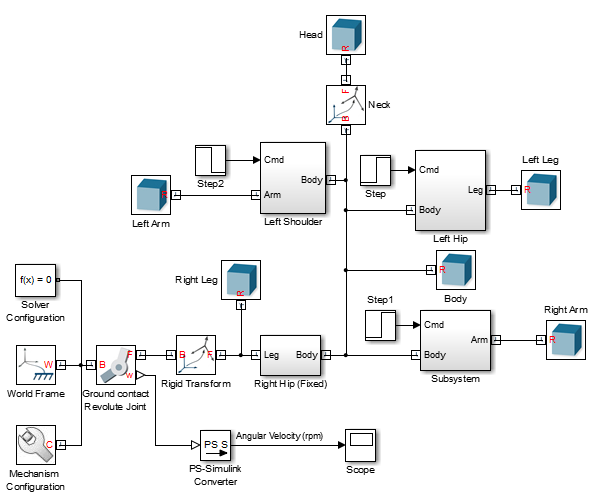
During the simulation, I first make the leg go down, accelerating the body a little. A few seconds after, I make both arms go closer to the body, reducing the moment of inertia and accelerating the body more significantly. Here is what it looks like:
Update: Download the models used in this post here:
Now it's your turn
Are you using Simulink to model and improve your sport performance? Let us know by leaving a comment here
- Category:
- Fun,
- Physical Modeling
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.