Olympics 2016 – Shot Put
For the Rio Olympics this year I decided to sign up a few of our new hires and interns to pick an Olympic sport and show what we can do in Simulink to simulate and analyze that sport.
Today, we are beginning with Alisha Schor, who implemented a simulation of the Shot Put using Simscape Multibody.
Introduction
In this post, we will investigate the mechanics of one Olympic event: the shot put. In the shot put, athletes compete to throw or “put” a round weight (7.26 kg for men, 4 kg for women) as far as they can, while still landing within the legal sector: an arc just under 35° in angle. The current world records are 22.63 m and 23.12 m for the women and men, respectively. You can read more about the rules here.
That’s quite a haul for something that weighs about a gallon of water (or two for the men). So how do they do it? Well, let’s take a look, and then we’ll see what else Simscape Multibody can tell us.
Three Phases
There are three main sources of power during a shot put. The first is to generate momentum by moving the entire body. This is done in one of two ways: the glide and the spin. Both are used, but the spin is the more common image conjured up when thinking about the shotput, whereby the thrower spins around within the throwing ring with the shotput on her shoulder. This generates angular momentum that is transferred to the shot upon release.
The second sort of power is the “preload” achieved by winding up the body prior to the throw. When the thrower releases, the elastic energy that was stored in his stretched muscles is returned to the shot. Finally, there is the actual put, in which the thrower pushes the implement as hard as possible.

The Model
Here is what the top level of the model looks like:

This model focuses on the spin and the push. To model the spin phase, we attached a Body block to a Revolute Joint. This is similar to the Olympic figure skater model from the last winter Olympics.
Using a series of Rigid Transforms and Revolute Joints, we implemented the shoulder, upper arm, elbow and lower arm. I decided to actuate the elbow and shoulder by motion. That way, we can focus on the kinematics of the throw, and measure the forces required to generate the motion to ensure they are realistic.
The tricky part is in the subsystem called "Lockable 6-dof Joint". During the spin and the put, the shot must move with the hand. Once this is complete, the shot must "fly" by itself until it hits the ground.
Simscape Multibody has a set of Constraints blocks, but those cannot be enabled and disabled during simulation as we need here. To implement the release of the shot, we use something similar to a stiff spring and damper, that we turn off when the shot gets released. For that, we sense the position and velocity of all the degrees of freedom of the 6dof Joint, multiply by stiffness and damping coefficients, and apply the results as forces and torques.

Control
Now that we have a moving arm and and spinning body, we need to figure out how to make it move.
Before going for an optimal move, I thought it would be convenient to use Stateflow to make a first quick test. Using a series of 4 states, we can make our thrower going through the phases of spinning, pushing with the shoulder, pushing with both elbow and shoulder, and releasing the ball.

As you can see below, it works! With a 10.12 meters shot, we are far from a gold medal, but it's a good start.
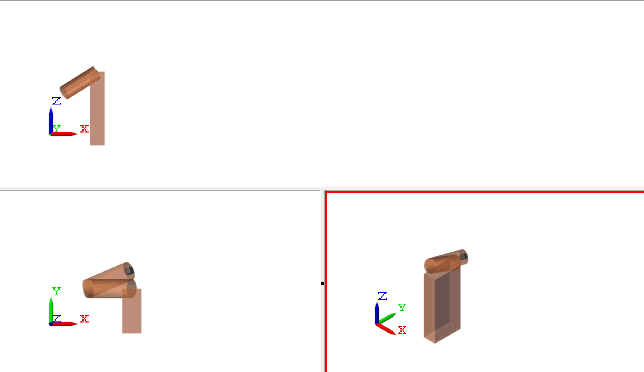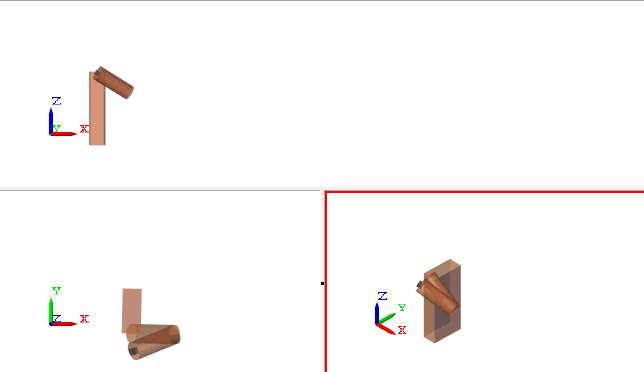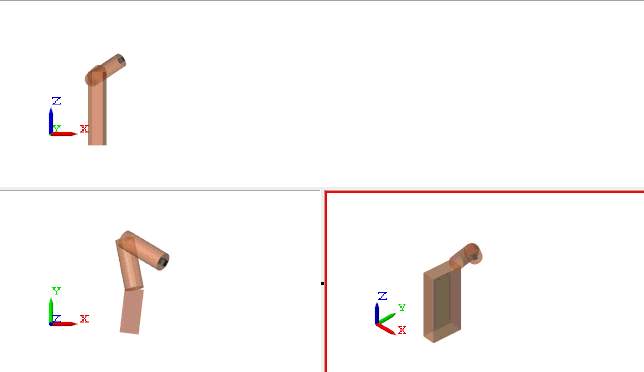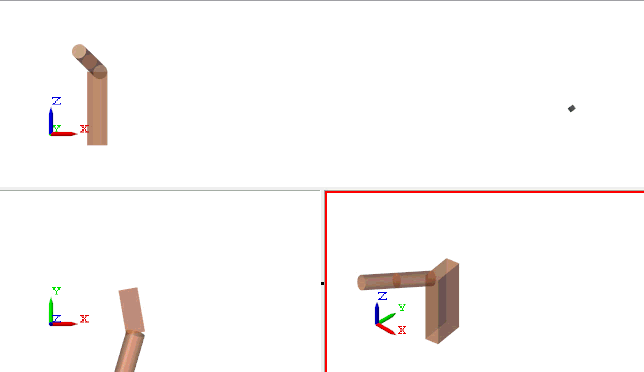
Now it's your turn
Anybody interested in designing the perfect throw?
Download the model, and give it a shot. I am sure this could make a very interesting optimization problem. I would start with fmincon to try maximizing the distance while respecting constraints like maximum torques at shoulder and elbow, and landing in the valid area. At the end, we should be able to reproduce a world record shot that looks like that:

Have fun, and enjoy the Olympics!
- Category:
- Challenge,
- Fun,
- Guest Blogger
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building






Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.