The Martian: Can you save Mark Watney? (Part 1)
About a year ago, I read the book The Martian, by Andy Weir. I really enjoyed the story, with all the technical details of how Mark Watney solves one problem after another to survive alone on Mars.
A few weeks ago, I realized that a movie with Matt Damon was coming out. After watching a few trailers, I ran into this YouTube video where Adam Savage (from the TV show MythBusters, among other things) interviews Weir.
In this video, Weir describes how he did not explicitly give the launch date of the Ares 3 mission in the book, but left enough clues for someone to figure it out.
As you can imagine, the nerd in me could not restrain itself from taking on that challenge. In this post, I will describe how one can use MATLAB to figure out the launch date of the Ares 3 mission.
Finding the launch date
In the book, we can find the following reference points:
- Thanksgiving: One of the main plot elements is that Mark Watney is able to extend his stay on Mars by growing potatoes. The potatoes he uses to start his crop were on board for a planned Thanksgiving dinner, which was supposed to happen on Sol 16 of their stay on Mars.
- Duration of the Earth-Mars trip: The book mentions that it took the Ares 3 crew 124 days to reach Mars.
- Radio Communication: On Sol 96 (80 earth days), Watney finds a way to communicate with Earth. It is mentioned that the communication delay on that day is 11 minutes.
As a rough estimation, let's say that Thanksgiving happens on November 25 every year. This means that the first communication happens on January 28th. I could probably have figured out that part without MATLAB, but let's see how we can do it with MATLAB:

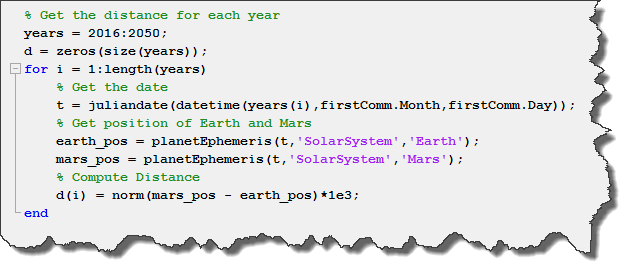
Then we need to know the positions of Earth and Mars around the Sun at a specific date. The Aerospace toolbox offers the function planetEphemeris that does exactly that:
We can then compare that data to the distance corresponding to the 11-minute communication delay:
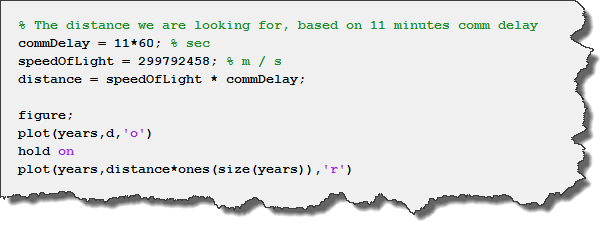
We find two possible candidate years: 2031 and 2036.

Using the planetEphemeris function again, we can refine our search and observe the motion of the two planets for those two years. Even though Earth and Mars are at the same distance on the communication date, day 204, there is no way a spaceship could reach Mars in 124 days in year 2030.

Turns out that Thanksgiving in 2035 will be on November 22 - which pegs the launch date around July 7-8. After coming up with that, I did a bit of googling and found many sites like insidescience.org and even a Facebook post by Andy Weir confirming that the Ares 3 mission launched July 7, 2035.
Yeah!
What's next? What about a little challenge?
Of course I could not stop here... we have not yet used Simulink!
Next week, I will describe how I put together a simulation in Simulink to design the trajectory of the spacecraft. Starting with the Planetary Orbit Due to Gravity example, I came up with a simulation including Venus, Earth, Mars, and the spacecraft. If you are interested, you can download the simulator here.
At first I played around with it, just for fun, trying to tweak the direction into which the constant-thrust engine delivers the 2 mm/s^2 of continuous acceleration. Then things got serious... But let's wait until next week for the details - we have seen enough for today.
Now it's your turn
Next week, I will describe how I put together the model that you can download here, and how I setup an optimization problem to design a trajectory that goes to Mars in 124 days and comes back to Earth after 365 days, per the original flight plan described in the book.
Until then, see if you can design a good trajectory yourself. For those who do not have SimMechanics, I included a protected version, so you can simulate the SimMechanics part, but not modify it. All you need to provide is a vector of time t and a vector of angles theta, between 0 and 360 degrees describing in which direction the constant-acceleration propulsion is pointing. The MAT-file included in the ZIP-file provides example t and theta, but those will not get you to Mars... Next week I will provide the result of the optimization.
Post your solution on MATLAB Central File Exchange and leave a comment here; I will present the most interesting solutions.
And if someone can come up with the full Rich Purnell Maneuver, I promise some excellent MathWorks swag!
Acknowledgement
I want to thank a few colleagues for helping with this blog post: Abhisek Roy, Jeevan Joishi, Subin Kuttappan, Vineeth Kartha, Amrit Sagar, and Tony Soares.

- Category:
- Challenge,
- Fun,
- Physical Modeling
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.